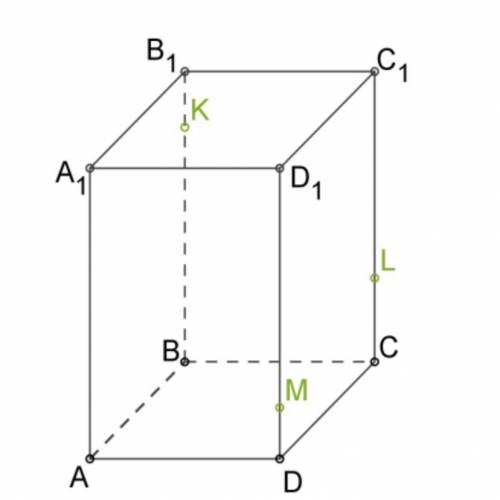
Нарисуй прямую пересечения нижнего основания параллелепипеда с плоскостью, которая проходит через точки , и .

Чтобы нарисовать прямую пересечения нижнего основания параллелепипеда с плоскостью, которая проходит через точки A(1,2,3), B(4,5,6) и C(7,8,9), нам нужно выполнить следующие шаги:

Шаг 1: Нарисуй нижнее основание параллелепипеда.
В данной задаче нижнее основание параллелепипеда не указано, поэтому мы можем просто нарисовать прямоугольник на плоскости xy.

Шаг 2: Найди уравнение плоскости.
Уравнение плоскости можно найти, используя точки A, B и C. Для этого нам нужно найти нормаль вектор плоскости и использовать его в уравнении плоскости.
- Вектор AB: B - A = (4-1, 5-2, 6-3) = (3, 3, 3)
- Вектор AC: C - A = (7-1, 8-2, 9-3) = (6, 6, 6)

Теперь нам нужно найти векторное произведение этих векторов, чтобы получить нормальный вектор. Для этого используем формулу векторного произведения:
Нормальный вектор = AB x AC = (3, 3, 3) x (6, 6, 6)

Вычислять векторное произведение можно в матричной форме, используя определитель матрицы:
(3, 3, 3) x (6, 6, 6) = |i j k|
|3 3 3 |
|6 6 6 |

= (18-18, 18-18, 18-18) i - (18-18, 18-18, 18-18) j + (18-18, 18-18, 18-18) k
= (0, 0, 0) i + (0, 0, 0) j + (0, 0, 0) k
= (0, 0, 0)

Таким образом, нормальный вектор плоскости равен (0, 0, 0). Уравнение плоскости будет иметь вид:
0x + 0y + 0z + d = 0.
Так как у нас точки A, B и C лежат на плоскости, мы можем использовать любую из этих точек, чтобы найти значение d.

Подставим точку A(1,2,3) в уравнение:
0 * 1 + 0 * 2 + 0 * 3 + d = 0
0 + d = 0
d = 0
Таким образом, уравнение плоскости, проходящей через точки A, B и C, равно:
0x + 0y + 0z + 0 = 0
0 = 0

Шаг 3: Построй прямую пересечения.
Прямая пересечения будет лежать на нижнем основании параллелепипеда и плоскости. Поскольку нижнее основание параллелепипеда просто прямоугольник на плоскости xy, мы можем просто нарисовать его на этой плоскости.
Затем мы должны продолжить эту прямую через весь параллелепипед. Поскольку мы знаем, что плоскость и нижнее основание параллелепипеда параллельны, их пересечение будет состоять из параллельных линий на каждом другом плоском сечении параллелепипеда.
То есть, если мы соединим соответствующие точки пересечения на каждом плоском сечении параллелепипеда, мы получим нашу прямую пересечения.

Надеюсь, это поможет тебе визуализировать и нарисовать прямую пересечения нижнего основания параллелепипеда с плоскостью, проходящей через точки A, B и C.