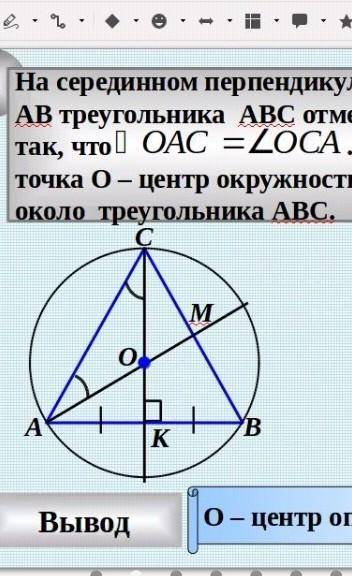
На серединном перпендикуляре стороны АВ треугольника АВС отмечена точка О та что ОАС равен ОСА. Докажите что точка О центр окружности описанной около треугольника АВС
Другие вопросы по теме Геометрия
Популярные вопросы
- Решите, производные) 1)(tg(2x+1)) 2)(ctgx+x) 3)(cosx^3) 4)(cos1/x^2) 5)(cos-корень...
3 - 25%от числа 48 составляют 3\4 числа m.найдите число m...
3 - Составить предложение со словом кезекшілік...
2 - Выполни деление с остатком и столбиком 73: 24= 98: 11= 95: 40= 78: 30= 1370:...
2 - Расставьте знаки препинания. раз шёл я по берегу нашего ручья и под кустом...
1 - Периметр прямоугольника равен 16,4 см одна из его сторон на 3,4 меньше другой...
2 - Расстояние от автобусного лагеря до автобусной остановки 29 км .успеют ли...
2 - Установите соответствие между признаками растения и семейством, к которому...
2 - Маша раскрыла атлас . каким членом предложения является слово атлас. а) подлежащее...
1 - Лесник посадили 178 елей , а тополей - 3 раза больше , чем елей . а кленовый...
3
т.О — центр описанной около ∆ АВС окружности, ч.т.д.
Объяснение:
В ∆ АОС углы при основании АС равны. Следовательно, ∆ АОС –равнобедренный, и АО=ОС.
В ∆ АОВ отрезок ОМ⊥АВ и делит её пополам. ⇒
ОМ высота и медиана ∆ АОВ. ⇒ ∆ АОВ — равнобедренный, и
АО=ОВ. Отрезки АО=ОВ=ОС
Точки А, В и С находятся на одном и том же расстоянии от О, следовательно, принадлежат окружности, так как ей принадлежит множество точек плоскости, находящихся на одном и том же расстоянии от одной точки, следовательно
(ответ сверху)