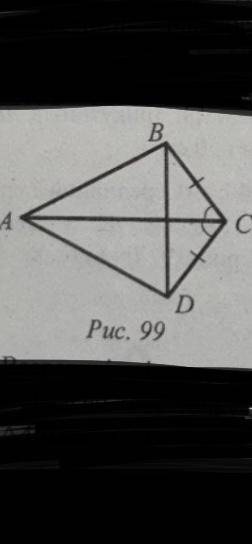
На рисунку 99 ВС=СD, Кут АСВ= куту АСD. Доведіть що трикутник АВD — рівнобедрений
До іть будь ласка
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. Діагоналі чотирикутника перетинаються в точці О. З точки О...
3 - Отгадать - спрягается/неспрягается...
1 - Конспект характеристика образов главных героев рассказа трофейная...
1 - Запишіть 5 слів або словосполучень, які б стали в природі для...
2 - Добрый вечер создать бизнес план ( бизнес автосалон) обществознание...
2 - 1. Кто является автором произведения «История Пугачевского бунта»?...
1 - К окружности с центром в точке О проведены касательная AB и секущая...
1 - Де випадає найбільше опадів(понад 2000мм)...
1 - Напишітьпрограму, в якій користувач вводить значення температури...
2 - 3. За до купрум (II) гідроксиду можна розпізнати такі пари речовин:...
1
Исходя из условия, у нас есть следующие данные:
- ВС = СD
- Угол АСВ равен углу АСD
Для начала, рассмотрим левую сторону треугольника АВD. У нас есть равенство ВС = CD. Это означает, что сторона ВС равна стороне CD, то есть они имеют одинаковую длину.
Теперь рассмотрим углы АСВ и АСD. У нас есть условие, что эти углы равны.
Используем свойство треугольника, которое гласит: "Если два угла треугольника равны, то и их противолежащие стороны равны".
Таким образом, поскольку угол АСВ равен углу АСD, значит, сторона АВ равна стороне АD.
Итак, мы доказали, что сторона ВС равна стороне CD и сторона АВ равна стороне АD. То есть треугольник АВD является равнобедренным.
Пропорции, однако, у нас нет, чтобы доказать это первой стороны равно второй, а второй третей, а третьей первой.