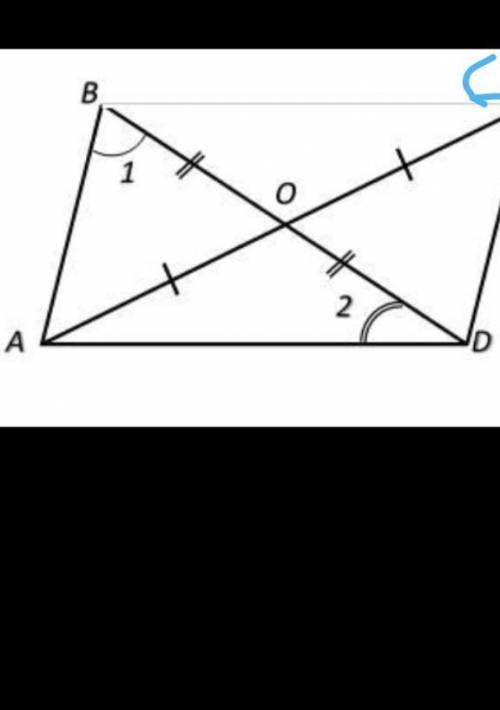
На рисунке OA=OC и OB=OD. Найдите ∠∠BDC, если ∠∠1=75градуса, ∠∠2=22 градуса

Чтобы найти угол ∠BDC, мы можем использовать свойство параллельных прямых, которое гласит, что если две прямые AB и CD параллельны и пересекаются третьей прямой, то сумма внутренних углов на одной стороне от пересечения равна 180 градусов.

В данном случае, прямые OA и CD параллельны, и они пересекаются прямой OB. Также известно, что ∠1 = 75 градусов и ∠2 = 22 градуса.

Первым шагом найдем угол COD. Так как OA = OC, то треугольники AOC и COD равнобедренные. Значит, угол COD равен углу ∠OCA, который равен ∠1 = 75 градусов.

Затем найдем угол OBD. Так как OB = OD, то треугольники OBD и OBD равнобедренные. Значит, угол OBD равен углу ∠OBD, который равен ∠2 = 22 градуса.

Теперь мы имеем углы ∠COD = 75 градусов и ∠OBD = 22 градуса. Сумма внутренних углов на стороне BDC равна 180 градусов, поэтому:

∠BDC = 180 - ∠COD - ∠OBD
∠BDC = 180 - 75 - 22
∠BDC = 83 градуса

Таким образом, угол ∠BDC равен 83 градусам.