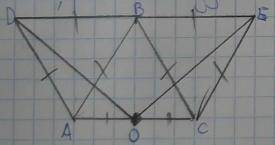
На боковых сторонах равнобедренного треугольника, во внешнюю сторону построены равносторонние треугольники. Докажите, что отрезки соединяющие вершины равносторонних треугольников (отличные от вершин равнобедренного) с середины основания равнобедренного треугольника, равны между собой. Доказать : DO = OE.
Другие вопросы по теме Геометрия
Популярные вопросы
- Скорость первого поезда 70 км/ч и за 1,5ч он проходит то же расстояние,...
2 - Какой частью речи является слово пятитонная...
2 - Сколько будет 987645235+342614465-888*5555555...
2 - Пластмаси, еластомери, хімічні волокна та полімерні покриття відносять...
1 - Составьте 10 во с ответами по содержанию третей части киниги Остров...
3 - Площадь Филиппинского моря 5.7млн км ^ 2.Какой процент Мирового океана...
2 - Берілген сұрақтардың біреуіне жауап беріңіз. Жауапты тиісті стильге...
3 - РЕШИТЬ ЗАДАЧИ Кокова сила тока в никелиновом реостате длиной 50м...Sсечения...
2 - Task1Complete the sentences using the negative or affirmative form of...
2 - (b+9-3a) РЕШИТЕЕ БЫСТОРО ОЧЕНЬ НУЖНО...
3
Объяснение:
1.Рассмотрим треугольник АВС (равнобедренный)
1) АВ=ВС
2.Так как треугольники АДВ и ВСЕ - равносторонние
Из 1) 2. Следует, что треугольники АДВ и ВСЕ равны
3.Отсюда :
1) АД=СЕ
2) АО=ОС
Углы ВАС и ВСА равны (по св-ву равнобедренных треугольников)
4. Углы ДАВ и ЕСВ - углы равнобедренного треугольника, значит ВАС +ДАВ = ВСА +ЕСВ = ДАС =ЕСА
Следовательно треугольники АДО и СЕО равны по двум сторонам и углы между ними
Из равенства следует, что ДО = ОЕ
Что и требовалось доказать