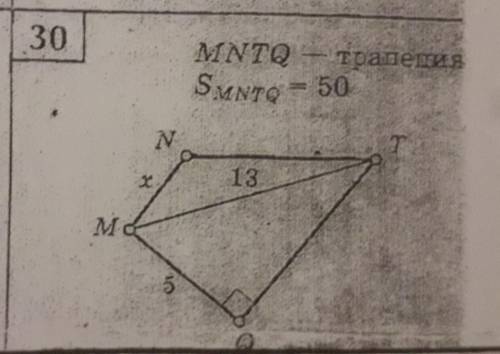
MNTQ прямоугольная трапеция площадь равна 50. Наименьшая боковая сторона MQ равна 5. Диагональ MT равна 13. Найти M
Другие вопросы по теме Геометрия
Популярные вопросы
- Блин, никогда не учила история Кто нарисован на картинке? А Княгиня...
3 - Придумайте название басни Кипящий Водопад, свергаяся со скал,Целебному...
1 - Синквейн к слову рижиссёр...
1 - Як формувались її погляди Єлизавети 1? ...
2 - как менялись персонажи Граф и Сильвио в повести выстрел? Почему Сильвио...
1 - сделать план рассказа Паустовского Корзина с еловыми шишками....
2 - Современный военно промышленный комплекс Казахстана реферат...
1 - написать рассказ о любом экзотическом животно, описать его фантастически...
2 - Какие меры предпринятые в петровскую эпоху коснулись христианства?...
1 - ДАЮ 35Б Зачет 8 класс Электромагнитные явления 1)Напряжение (определение,...
3
У нас дана прямоугольная трапеция MNTQ. Мы знаем, что ее площадь равна 50, наименьшая боковая сторона MQ равна 5, а диагональ MT равна 13. Наша задача - найти значение M.
Для начала обратимся к формуле для площади трапеции: площадь трапеции равна половине произведения суммы ее оснований и ее высоты.
Так как у нас прямоугольная трапеция, то одно из ее оснований - это основание с наименьшей длиной, то есть MQ. Другое основание - NT. Поэтому площадь нашей трапеции можно выразить следующим образом:
50 = (MQ + NT) * высота / 2
Теперь нам нужно найти высоту трапеции. Для этого воспользуемся теоремой Пифагора. Рассмотрим прямоугольный треугольник MTQ. У него известны гипотенуза MT (13) и катет MQ (5). По теореме Пифагора можно найти второй катет - высоту треугольника (высоту трапеции).
Применим теорему Пифагора:
MT^2 = MQ^2 + высота^2
13^2 = 5^2 + высота^2
169 = 25 + высота^2
высота^2 = 144
высота = 12
Вернемся к нашему уравнению для площади трапеции и подставим полученное значение высоты:
50 = (5 + NT) * 12 / 2
Упрощаем:
50 = (5 + NT) * 6
Теперь решим полученное уравнение относительно NT:
50 = 6 * NT + 30
20 = 6 * NT
NT = 20 / 6
NT = 10/3
Таким образом, второе основание NT равно 10/3.
Итак, мы знаем значения обоих оснований трапеции: MQ = 5 и NT = 10/3.
Осталось найти значение M, которое является вершиной трапеции.
Для этого мы можем воспользоваться свойством противоположных углов: сумма углов MTQ и MNT равна 180 градусов. Угол MTQ прямой, поэтому угол MNT (угол M) также будет прямым.
Теперь мы можем использовать теорему Пифагора в прямоугольном треугольнике MNT:
M^2 + NT^2 = MT^2
M^2 + (10/3)^2 = 13^2
M^2 + 100/9 = 169
M^2 = 169 - 100/9
Упрощаем:
M^2 = (1521 - 100) / 9
M^2 = 1421 / 9
Теперь найдем значение M, извлекая квадратный корень из обоих сторон:
M = √(1421 / 9)
M ≈ 11.309
Таким образом, ответ: значение M примерно равно 11.309.