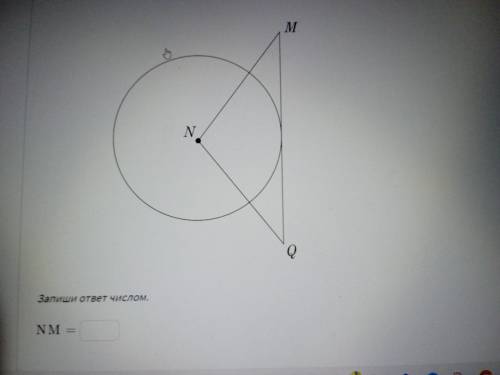
M Q - касательная к окружности с центром N и радиусом 10. Найдите значение NM , если MQ = 48 найдите NM

Для решения данного вопроса, нам понадобится использовать свойства касательных и окружностей.

Если M Q является касательной к окружности с центром N и радиусом 10, то мы можем использовать теорему о касательной и хорде.

Согласно этой теореме, когда касательная M Q и хорда NM пересекаются, произведение длин отрезков M Q и MN равно квадрату длины NM ( M Q ∙ M N = N M 2 ).

Таким образом, у нас есть следующее уравнение:

48 ∙ M N = N M 2

Для решения этого уравнения, нам нужно найти значение длины NM . Для этого, давайте решим уравнение:

48 ∙ M N = N M 2

Сначала делим обе стороны на 48:

M N = N M 2 / 48

Теперь давайте возведем обе стороны в квадрат, чтобы избавиться от квадрата на правой стороне:

M N 2 = ( N M 2 / 48 ) 2

Сократим квадрат на правой стороне:

M N 2 = N M 4 / ( 48 2 )

Сократим квадраты соответствующим образом:

M N 2 = N M 4 / 2304

Теперь у нас есть уравнение, в котором неизвестное значение NM является частью данного уравнения. Чтобы найти конкретное значение NM , нам нужно знать дополнительную информацию или использовать дополнительные уравнения или свойства.

Возможно, вам нужно дополнительные данные или информацию для полного решения этой задачи. На основании только предоставленной информации, мы не можем определить конкретное значение NM.

Однако, если у нас есть дополнительные детали или условия, будьте добры предоставить их, чтобы я мог помочь вам решить задачу.