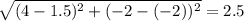Любую из задач, желательно все

Другие вопросы по теме Геометрия
Популярные вопросы
- Өтініш,барлық сұрақтарға жауап бере аласыздар ма?...
1 - 1.Что такое триумвират? 2. Что означает фраза «жребий брошен»? 3.Когда была установлена...
3 - Определи тип текста: Эксперты Всемирной метеорологической организации не связывают...
3 - Выберите Present Perfect Passive (PP) или Present Perfect Progressive (PPP).1. Our...
3 - Памагите мне нада ришит скока бует 2 плюс памагит! быстро!...
1 - У выражение:а) 6a(2a + 3b) – 2b(6a – 2b); б) 4с(с – 4)2 + (2с...
1 - 1. Пользуясь циркулем и линейкой, начертите окружность с центром О и произвольным...
3 - Приведите 3 примера развития экономики в результате реформы Мэйдзи в Японии ? ОТВЕТЬТЕ...
2 - Сделайте что сможете и с полным решением...
2 - Напишите 2 небольших рассказа Мои любимые вещества (об 1-м и 1-м сложном)...
1
1. S=l×h, где l - средняя линия
S= 15×9=135
ответ: 135дм^2
2. Так как DE||AC и DE делит BC пополам - отсюда следует, что DE - средняя линия, значит она и сторону AB делит пополам, отсюда следует что AD=DB
3. пусть АК медиана, K(x;y) середина ВС
Найдем координату середины отрезка ВС
х=(1+2)/2=3/2=1,5
y=(-4+0)/2=-2
А теперь найдем длину АК
АК^2=(4-1,5)^2+(-2+2)^2=2,5^2
AK=2,5
Объяснение:
1) средняя линия - полусумма оснований * высоту, полусумма оснований - средняя линия, площадь: 15 * 9 = 135 дм²
2) ΔBED подобен треугольнику ΔВAC по первому признаку (∠ABC = ∠DBE - совпадают, ∠DEB = ∠ACB как соответствующие при параллельных прямых) Значит, BC/BE = BA/BD = 2 (BC в 2 раза больше BE = EC). Тогда AB = 2BD = BD + DA ⇒ DA = BD, что и требовалось доказать.
3) середина BC: D((1+2)/2, (-4+0)/2) = D(1.5, -2). Расстояние от A до D: