Кто чем может 1. периметр равнобедренной трапеции равен 60 см. ее боковая сторона равна меньшему основанию и в два раза меньше большего основания. найдите среднюю линию трапеции. 2. в треугольнике авс ∠ c = 20 ∠ b = 115, высота вн равна 8 см. найдите на. 3. во сколько раз увеличится площадь круга, если длину ограничивающей его окружности увеличить в 3 раза?
Другие вопросы по теме Геометрия
Популярные вопросы
- Решите измерения прямоугольного параллепипеда abcda1b1c1d1 равны 3,4 и корень...
2 - Замените данные уравнения равносильными уравнениями вида ax=b a) 8x+15=39...
2 - Алдаркосе персонаж казакских сказок сын бедняка находчивый и хитрый алдаркосе...
3 - Как расположить координатные точки: k(-7.4),n(-7.005),l(-7.5/8),m(-7.3/5)....
1 - Укаждого из трёх охотников по 6 коробок пуль по 20 пуль. сколько всего пуль...
1 - Азақ тілі 8 сынып 20бет 4 тапсырма...
1 - Как записать условие : у каждого из 3 охотников по 6 коробок по 20 штук в...
1 - 40 5 класс зарубежканапишите, , пересказ любой европейской сказки про ...
2 - Решите эти примеры a) -3(6,1x+0,3y)-12x. b) -(-1,3x+8y)+(-4x-1,1y). и эти...
2 - Продолжи ряд: 0,3; 0,5; 0,9; 1,7; 3,3; 6,5;...
1
1) P=60
боковая сторона = меньшее основание = большее основание/2 = x
60 = x+x+x+2x = 5x
x=12
большее основание = x*2=24
средняя линяя = (большее основание + меньшее основание)/2 = (12+24)/2=18
2) угол CBH = 180-90-20=70 градусов =>
угол HBA = 115-70=45 градусов
угол HBA = угол A => BH=HA=8
3)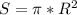
т.е.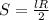
следовательно при увеличении длины окружности, её площадь также увеличится в 3 раза