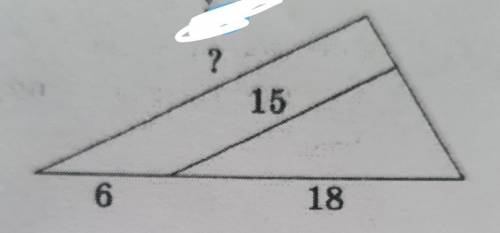
Используя данные, указанные на рисунке, найдите
неизвестную сторону треугольника.​

ответ:  x=20.

Объяснение:

Решение.

Из подобия треугольников следует отношение

15/18 = х/(18+6);

x=15*24/18 = 20;

x=20.

На рисунке дан правильный треугольник ABC, где сторона BC имеет неизвестную длину.

Чтобы найти длину стороны BC, мы можем использовать теорему Пифагора. Эта теорема гласит, что квадрат длины гипотенузы равен сумме квадратов длин катетов.

В нашем случае, сторона AC является гипотенузой треугольника, а стороны AB и BC - катетами.

Таким образом, мы можем записать уравнение на основе теоремы Пифагора:

AB^2 + BC^2 = AC^2.

Для решения этого уравнения нам нужно знать длины сторон AB и AC.

Согласно рисунку, сторона AB равна 8 см, а сторона AC равна 10 см.

Подставим эти значения в уравнение:

8^2 + BC^2 = 10^2.

64 + BC^2 = 100.

Теперь вычтем 64 из обеих сторон уравнения:

BC^2 = 100 - 64.

BC^2 = 36.

Чтобы найти BC, возьмем квадратный корень от обеих сторон уравнения:

BC = √36.

BC = 6.

Таким образом, неизвестная сторона треугольника BC равна 6 см.