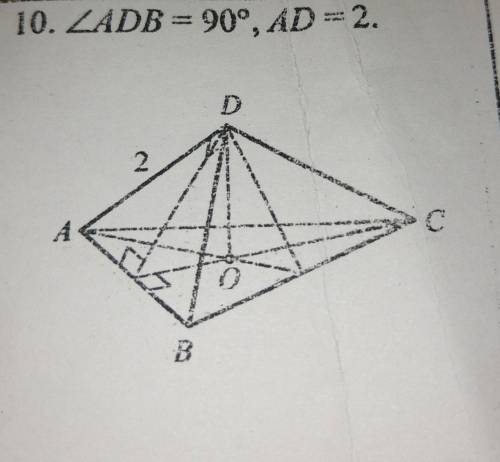
геометрия дано: правильная пирамида, угол ADB=90° , AD=2. найти площадь боковой поверхности. в фото можете посмотреть

буду очень вам благодарна

Чтобы найти площадь боковой поверхности правильной пирамиды, необходимо знать ее высоту и периметр основания. Поскольку в задании дано значение угла ADB и значение стороны AD, мы можем вычислить высоту пирамиды по теореме Пифагора. Для начала, обратим внимание на треугольник ADB на рисунке. Мы можем использовать теорему Пифагора (a^2 + b^2 = c^2), чтобы найти значение DB (гипотенуза). Из условия задачи, известно, что AD = 2, а угол ADB равен 90 градусам. Таким образом, мы можем выразить значение DB через AD: DB^2 = AD^2 + AB^2 DB^2 = 2^2 + AB^2 DB^2 = 4 + AB^2 Теперь посмотрим на треугольник ABC. Мы знаем, что его угол BCA равен 90 градусам, поэтому треугольник ABC является прямоугольным. Следовательно, мы можем использовать теорему Пифагора для вычисления стороны AB: AB^2 = AC^2 + BC^2 Из условия задачи, мы знаем, что сторона AC равна 4. Будучи равнобедренным треугольником, треугольник ABC имеет равные значения сторон AB и BC. Поэтому мы можем записать: AB^2 = 4^2 + BC^2 AB^2 = 16 + BC^2 Теперь мы можем объединить эти два уравнения: DB^2 = 4 + AB^2 DB^2 = 4 + (16 + BC^2) DB^2 = 20 + BC^2 Таким образом, мы выразили значение DB через BC: DB^2 = 20 + BC^2 DB^2 - BC^2 = 20 Теперь, имея значение DB, мы можем найти значение высоты пирамиды. Высота пирамиды (h) будет равна DB. Это связано с тем, что высотой пирамиды является перпендикулярная линия от вершины пирамиды до основания, проходящая через середину стороны основания. Таким образом, h = DB. Итак, мы получили значение h^2 = DB^2 - BC^2 = 20. Теперь, зная значение высоты пирамиды, нам нужно найти периметр основания пирамиды. Обратите внимание, что основание пирамиды в данном случае представляет собой правильный треугольник ABC. Периметр правильного треугольника может быть найден путем умножения длины любой из его сторон на 3. У нас уже есть значение стороны AB, которое равно 4. Таким образом, периметр основания пирамиды (P) будет равен 3 * AB. P = 3 * AB P = 3 * 4 P = 12 Теперь, используя значение периметра основания и высоты пирамиды, мы можем найти площадь боковой поверхности пирамиды. Формула для площади боковой поверхности правильной пирамиды - S: S = (1/2) * P * h где P - периметр основания, h - высота пирамиды. В нашем случае: S = (1/2) * 12 * DB S = 6 * DB Теперь мы можем найти значение DB из предыдущего уравнения: DB^2 - BC^2 = 20 К сожалению, без значений сторон BC и AB, мы не можем выразить значение DB и, следовательно, найти площадь боковой поверхности пирамиды. Таким образом, без дополнительной информации о пирамиде мы не можем найти точное значение площади боковой поверхности.