Дорогие геометрики мне, аминь... ​

АД =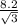  

Периметр ΔАОД = 8,2√3

Объяснение:

ΔАОД - равнобедренный (ОА=ОД=R), т.к. АВ=ВД (В - середина АД), то ОВ - медиана. Медиана в равнобедренном Δ является также высотой ⇒ОМ⊥АД.

Четырёхугольник АОДМ: Диагонали перпендикулярны, а если диагонали выпуклого четырехугольника взаимно перпендикулярны, то суммы квадратов его противолежащих сторон равны:

АО²+ДМ²=ОД²+АМ²

АО=ОД=R ⇒ R²+ДМ²=R²+АМ²

⇒ДМ=АМ ⇒ Четырёхугольник АОДМ - ромб,

ОА=ОД=ДМ=АМ=R

Рассмотрим ΔАОВ(∠В=90°). ОВ=1/2ОМ (св-во диагоналей ромба)

ОМ=1/2 ТМ ⇒ ОВ=1/4 ТМ = 1/4* 16,4 = 4,1 см

∠О=30°.

ОА=R=ОВ/cos 30° = =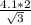

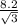
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.

АВ=1/2 ОА = 1/2 *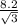  = 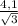, т.к. В - середина АД, то

АД = 2*АВ=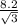

Периметр ΔАОД = 2*ОА+АД= 2*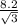 + 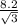= 8,2√3