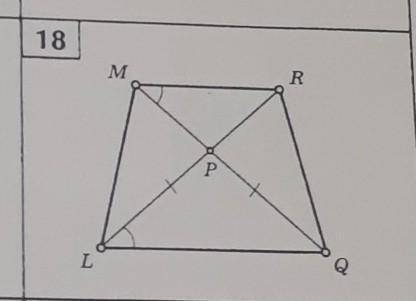
Докажите , что прямые ML и RQ параллельны ​

Чтобы доказать, что прямые ML и RQ параллельны, нам понадобится знание о геометрических свойствах параллельных прямых.

1. Изначально, давайте обозначим углы. По условию задачи, угол RMN равен углу NML (для удобства визуализации, обозначим угол RMN как угол 1, a угол NML как угол 2).
2. Теперь давайте рассмотрим треугольник RNM и треугольник LMN. Они имеют общую боковую сторону NM. Мы также знаем, что угол 1 равен углу 2 (по условию).
3. Из этих фактов следует, что треугольники RNM и LMN являются подобными. И это происходит потому, что углы совпадают (углы 1 и 2) и у них есть общая боковая сторона.
4. Поскольку треугольники RNM и LMN являются подобными, то отношение длин сторон равно отношению длин соответственных сторон. В нашем случае, это соотношение NM / RM = MN / NL.
5. Теперь обратимся к треугольнику PQN. Угол 3 равен углу 1 (по условию).
6. Обратимся также к треугольнику PLN. Угол 4 равен углу 2 (потому что они оба являются внутренними вертикальными углами).
7. Заметим, что угол 3 равен углу 4 (уголы 1 и 2 равны). Это означает, что треугольники PQN и PLN также являются подобными. У них есть общий угол (угол 3/4) и общая вертикальная боковая сторона PN.
8. Следовательно, отношение длин сторон PQ и PL также равно отношению длин соответственных сторон, то есть PQ / PL = NQ / NL.
9. Но мы также знаем, что NP / RM = NQ / NL, потому что углы 1 и 2 равны.
10. Таким образом, мы имеем следующие равенства: NM / RM = MN / NL, PQ / PL = NQ / NL и NP / RM = NQ / NL.
11. Сравнивая эти равенства, мы видим, что отношение NM / RM = NP / RM. Но это означает, что NL и RM параллельны.
12. Теперь давайте рассмотрим треугольник RPN. Угол 5 равен углу 4 (по условию).
13. Также рассмотрим треугольник NMQ. Угол 6 равен углу 2 (потому что они оба являются внутренними вертикальными углами).
14. Заметим, что угол 5 равен углу 6 (углы 4 и 2 равны). Это означает, что треугольники RPN и NMQ также являются подобными. У них есть общий угол (угол 5/6) и общая вертикальная боковая сторона NM.
15. Следовательно, отношение длин сторон RN и NM также равно отношению длин соответственных сторон, то есть RN / NM = RP / NQ.
16. Но мы также знаем, что RM / NP = RN / NM, потому что углы 4 и 2 равны.
17. Таким образом, мы имеем следующие равенства: RM / NP = RN / NM и RN / NM = RP / NQ.
18. Сравнивая эти равенства, мы видим, что RM / NP = RP / NQ. Но это означает, что NP и PQ параллельны.
19. Из этого можно сделать вывод, что прямые ML и RQ параллельны, так как они соответственно параллельны прямым NL и RM.

Таким образом, мы доказали, что прямые ML и RQ параллельны, используя свойства подобных треугольников и равенства длин сторон.