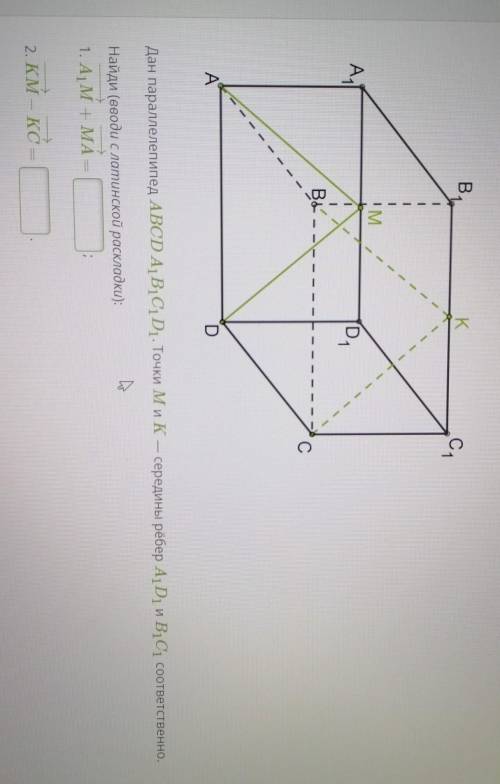
Дан параллепипед АВСDА1В1С1D1. Точки М и К середины рёбер А1D1 и В1С1 соответственно. Найди:
А1М+МА=
КМ- КС=
Другие вопросы по теме Геометрия
Популярные вопросы
- Розрахувати Mr вищого оксиду елемента R, якщо відома Mr його сполуки е Гідрогеном:...
2 - Какое число нужно вставить вместо х, чтобы получилось верное равенство 26...
2 - Описать 3 указателя на символьный тип. Выделить для них динамическую память....
1 - Равнобедренная трапеция OPRS с основаниями PR и OS описания около окружности...
1 - 3. Сероводород не реагирует с*1) Cus2) КОН3) O24) 12...
3 - Определите эквивалент для кислоты: Н4[Fe(CN)6]...
3 - Поясніть взаємозалежність між безпекою й статевою культурою ...
1 - Чоловік, який має короткі вії, одружився з жінкою, яка має довгі вії. У них...
1 - ХЭЭЭЭЭЭЭЭЭЛП! ОЧЕЕЕНЬ МАЛО ВРЕМЕНИ У МЕНЯ! Если можете то решение напишите!...
1 - Определить силу тяжести медного бруска объемом 250 см3...
3
Заметим, что вершины параллелепипеда образуют среднюю линию параллелограмма А1В1С1D1. Точка М - середина ребра А1D1, а точка К - середина ребра В1С1. Так как средняя линия делит диагонали параллелограмма пополам, то между вершинами А1 и М, а также между вершинами М и А, существует равенство длин. Аналогично, между вершинами К и М, а также между вершинами М и К, существует равенство длин.
Итак, мы можем написать следующие равенства:
А1М = МА (ребро А1D1 делится точкой М пополам)
КМ = МК (ребро В1С1 делится точкой К пополам)
Подставим значения А1М и КМ в уравнения и упростим:
А1М + МА = 2МА
КМ - КС = МК - КС = МС
Таким образом, ответ на вопрос будет:
А1М + МА = 2МА
КМ - КС = МС
Надеюсь, ответ был понятен и подробен! Если возникнут дополнительные вопросы, не стесняйтесь задавать их.