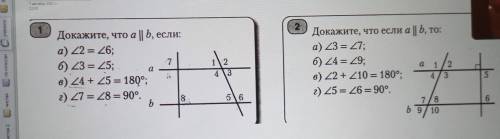
докажите, что a || b, если: a) угол 2= углу 6 b) угол 3= углу 5 в) угол 4 + угол 5=180 градусов г) угол 7=углу 8=90 градусов

а) 2 признак рав.пр.

б) 1 признак рав.пр.

в) 3 признак рав.пр.

г) признак прямых, перпендикулярных одной прямой.

Объяснение:

Док-во:

а) углы 2, 6 (соответственные и т.к. они равны, по условию, то и а||b - по 2-ому пр.)

б) углы 3, 5 (внутр.накрест лежащие и т.к. они равны, то а||b - по 1-ому пр.)

в) углы 4+5=180° (внутр. односторонние и т.к. их сумма равна 180°, то а||b - по 3-ему пр.)

г) углы 7, 8 имеют значение в 90°, то секущая (например с) является перпендикуляром, то соответственно а||b (св. прямых, перпендикулярных одной прямой).

Для доказательства, что линии a и b параллельны, мы должны использовать факт, что если у нас есть две пары соответственных углов, то линии параллельны.

В данном случае, чтобы доказать, что a и b параллельны, мы должны показать, что углы 1 и 2 являются соответственными углами.

Давайте разберемся:

Из условия, угол 2 и угол 6 равны. Поэтому, мы можем записать это как:

угол 2 = углу 6 (условие a)

Также, из условия, угол 3 и угол 5 равны:

угол 3 = углу 5 (условие b)

Теперь, мы знаем, что угол 2 и угол 6 равны. Из геометрической аксиомы, соответственные углы равны при пересечении двух параллельных линий. Поэтому, мы можем сделать вывод, что угол 1 и угол 5 равны (так как они являются соответствующими углами при пересечении линий a и b):

угол 1 = угол 5

Теперь, мы знаем, что угол 3 и угол 5 равны. Мы также знаем, что угол 4 и угол 5 образуют смежные углы (углы, которые имеют общую сторону и общую вершину). Из геометрической аксиомы, сумма смежных углов равна 180 градусов. Поэтому, мы можем записать это как:

угол 4 + угол 5 = 180 градусов (условие в)

Итак, мы имеем угол 1 = угол 5 из предыдущего вывода и угол 4 + угол 5 = 180 градусов из условия в.

Теперь, мы можем объединить эти два уравнения, чтобы получить:

угол 1 + угол 4 = 180 градусов

Мы также знаем, что угол 7 = углу 8 = 90 градусов (условие г).

Теперь, мы можем сделать вывод, используя геометрическую аксиому, что если сумма углов в одном треугольнике равна 180 градусов, то этот треугольник прямоугольный. Поэтому, используя угол 7 = углу 8 = 90 градусов, мы можем сказать, что треугольник 7-4-3 является прямоугольным треугольником.

Таким образом, мы приходим к выводу, что углы 1 и 2 являются соответственными углами и треугольник 7-4-3 является прямоугольным треугольником.

Следовательно, по геометрическому свойству, линии a и b параллельны.