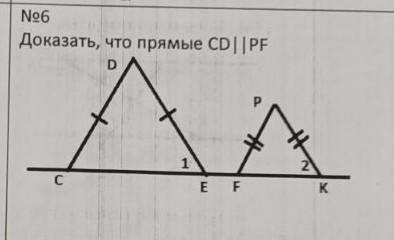
Доказать что прямые CD параллельны PF
​

Для доказательства того, что прямые CD параллельны PF, мы можем использовать два подхода - геометрические свойства параллельных прямых и равенство углов.

Подход 1: Использование геометрических свойств параллельных прямых.

1. По условию задачи, дан треугольник AFB, в котором точка C лежит на стороне AB.

2. Мы знаем, что когда прямые AB и CD пересекаются, сумма углов, образованных прямыми с пересекающей прямой, равна 180 градусов (т.е. углы 1 и 2 равны 180 градусов).

3. Рассмотрим треугольник CFD. Он также имеет две параллельные стороны - CD и PF.

4. Если прямые CD и PF параллельны, то сумма внутренних углов треугольника CFD также будет равна 180 градусов.

5. Теперь посмотрим на углы 3 и 4. Угол 3 - внутренний угол треугольника CFB, а угол 4 - внешний угол треугольника CFD. По свойству параллельных прямых, внутренние и внешние углы, образованные прямыми с пересекающей прямой, дополняют друг друга (т.е. сумма углов 3 и 4 равна 180 градусов).

6. Таким образом, углы 3 и 4 в треугольнике CFD, а также углы 1 и 2 в треугольнике AFB, равны 180 градусов.

7. Так как углы треугольника CFD и треугольника AFB в сумме дают 360 градусов, то можно заключить, что прямые CD и PF параллельны.

Подход 2: Использование равенства углов.

1. Рассмотрим треугольник CFB.

2. Угол CFB - внутренний угол треугольника.

3. Являющиеся продолжением прямых AC и FB, прямые CD и PF пересекаются в точке F.

4. Согласно основной теореме о параллельных прямых (если две прямые, пересекаемые третьей прямой, образуют одинаковые углы с этой прямой, то они параллельны), чтобы доказать, что прямые CD и PF параллельны, необходимо доказать, что углы CFB и CPF равны.

5. Мы должны показать, что углы CFB и CPF равны друг другу.
- Угол CFB можно обозначить через а.
- Угол CPF можно обозначить через b.

6. Обратим внимание на то, что углы CFB и CPF являются вертикальными углами, так как они образованы пересекающимися прямыми CD и PF.

7. По свойству вертикальных углов, вертикальные углы равны между собой.

8. Таким образом, углы CFB и CPF равны, что означает, что прямые CD и PF параллельны.

В результате обоих подходов, мы доказали, что прямые CD и PF параллельны.