1. Геометрия
  2. Диагонали трапеции abcd с

Диагонали трапеции abcd с основаниями ad и bc пересекаются в точке о. а) докажите, что площади треугольников аов и соd равны. б) в треугольнике cod проведена высота oh = 6, причем ch = 3, угол doh в 2 раза больше угла coh. найдите площадь треугольника doh. с б

kristinakuleh kristinakuleh    2   30.03.2019 13:00    4

Ответы
kermantanja kermantanja  27.05.2020 17:25

Т.к. ОН - высота треугольника, то ОНС - прямоугольный. Найдём ОС по теореме Пифагора

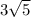
OC = \sqrt{OH^{2}+HC^{2} } = 3\sqrt{5}

Найдём синус и косинус угла НОС

sinHOC=HC/OC=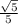\frac{\sqrt{5} }{5}

cosHOC=OH/OC=\frac{2\sqrt{5} }{5}

Т.к. по условию, угол DOH = 2 углам COH, то sinDOH=2*sinCOH*cosCOH

sinDOH=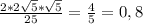\frac{2*2\sqrt{5}*\sqrt{5} }{25} =\frac{4}{5}=0,8

Из основного тригонометрического тождества найдём cosDOH

cosDOH=\sqrt{1-sin^{2}DOH } =0,6

cosDOH=OH/OD ==> OD=OH/cosDOH=6/0,6=10

Тогда DH из теоремы Пифагора равна - 8

Sdoh=0,5*OH*DH=0,5*6*8=24

ответ 24

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
gal12 gal12  20.08.2019 06:40
Втругольнике авд проведена биссектриса вс. угол д=45 градусов , угол всд=100 градусов найти угол а...
rogozhin0 rogozhin0  29.05.2019 15:50
Вокружности с центром в точке о проведена хорда ab. центральный угол aob равен 105 градусов.через точки a и b проведены касательные к окружности,пересекающиеся в точке...
violapi violapi  29.05.2019 15:50
Диагонали ас и bd прямоугольника abcd пересекаются в точке аю ао=13, а ав: вс=5: 12. найдите cd...
nikitos196 nikitos196  29.05.2019 15:50
Найти углы равнобедренного треугольника, если известно, что найдется прямая, проходящая через вершину угла при основании, делящая исходный треугольник на два равнобедренных?...
alusik2005 alusik2005  29.05.2019 15:50
Втреугольнике mnk стороны mn=20, nk=18, внешний угол при вершине n равен 150. найдите высоту, проведенную к стороне mn?...
Вовка753 Вовка753  29.05.2019 15:50
Втреугольнике авс стороны ас и вс равны 5, ав =2√21. найдите sin а. с подробным объяснением,...
сюрприз23456789 сюрприз23456789  29.05.2019 15:50
Высота прямоугольного треугольника, проведённая из вершины прямого углак гипотенузе, равна 4√3. один из катетов равен 8. найдите площадь исходного треугольника....
vvasea66 vvasea66  04.06.2020 16:56
А) Точки A(4;2;-1), С(-4;2;1), D(7;-3;4) - вершины параллелограмма ABCD. Найдите координаты четвертой вершины параллелограмма. б) Доказать, четырехугольник ABCD - прямоугольник,...
denis403 denis403  04.06.2020 16:57
Вариант A1 номер 3. и лайк ставлю. Заранее...
поплрадДРм поплрадДРм  05.06.2020 16:58
Башня высотой 60 м видна из некоторой точки на местности под углом 30 градусов. Расстояние от этой точки до основания башни примерно равно НАПИШИТЕ РЕШЕНИЕ ОТВЕТ БУДЕТ...

Популярные вопросы