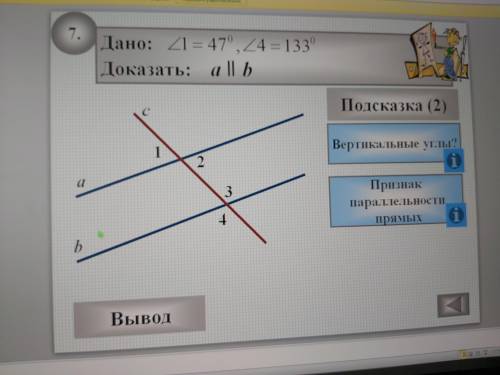
Дано: угл 1 = 47°, угл 4 = 133°
Доказать:a||b

ответ: таки да, параллельны! Воистину возрадуемся братья тому, что чудеса случаются!

Объяснение:

во вложенном файле.

Для доказательства, что прямые a и b параллельны, нам необходимо найти доказательства, основываясь на заданных углах.

Шаг 1: Изначально у нас есть два угла: угол 1 (47°) и угол 4 (133°).

Шаг 2: Посмотрим на прямую a и найдем ее углы. Угол 1 является внутренним углом a, поэтому он должен быть равен дополнительному углу 2. Используем свойство внутреннего угла прямой:

угол 2 = 180° - угол 1
угол 2 = 180° - 47°
угол 2 = 133°

Шаг 3: Теперь обратимся к прямой b и найдем ее углы. Угол 4 является внутренним углом b, поэтому он должен быть равен дополнительному углу 3. Используем свойство внутреннего угла прямой:

угол 3 = 180° - угол 4
угол 3 = 180° - 133°
угол 3 = 47°

Шаг 4: Заметим, что угол 2 и угол 3 оказались равными 133° и 47° соответственно. Мы знаем из свойства, что если углы, образованные двумя пересекающимися прямыми и третьей пересекающейся прямой, равны между собой, то две прямые параллельны. В нашем случае угол 2 и угол 3 равны, значит прямые a и b параллельны.

Итак, мы доказали, что прямые a и b параллельны, используя заданные углы 1 и 4.