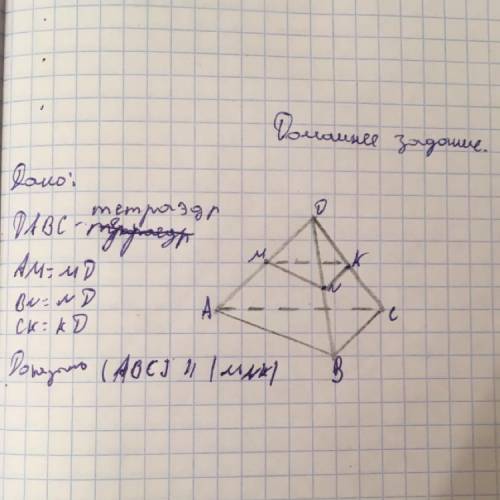
Дано:
DABC-тетраэдр
AM=MD
BN=ND
CK=KD
Доказать: ABC параллельна MNK

Для решения данной задачи, мы должны использовать знания о параллельности плоскостей. Докажем, что плоскость ABC параллельна плоскости MNK, используя данные, которые у нас уже есть.

Возьмем отрезки AM и MD. По условию задачи, AM = MD, что означает, что отрезки AM и MD равны по длине. Это говорит о том, что точка D делит отрезок AM пополам.

Теперь обратимся к отрезкам BN и ND. По условию задачи, BN = ND, что значит, что отрезки BN и ND равны по длине. Это подразумевает, что точка D делит отрезок BN пополам.

То же самое можно сказать и о отрезках CK и KD, т.е. CK равен KD и точка D делит отрезок CK пополам.

Исходя из данной информации, мы можем сделать вывод, что точка D является центром масс отрезков AM, BN и CK. В тетраэдре DABC это означает, что точка D является центром плоскости ABC.

Теперь давайте рассмотрим отрезки DM и DK. Поскольку D является центром масс отрезков AM и CK, а D делит отрезки AM и CK пополам, отрезки DM и DK должны быть равными.

Далее, рассмотрим треугольники DMB и DKC. Они имеют равные углы при вершине D, так как отрезки DM и DK равны, а они являются противлежащими сторонами смежных углов ABC и MNK. Таким образом, треугольники DMB и DKC подобны.

На основании этого мы можем сделать вывод, что углы ABC и MNK равны, так как это соответствующие углы подобных треугольников.

Таким образом, мы доказали, что плоскость ABC параллельна плоскости MNK, потому что углы между прямыми AB и MN, BC и NK, а также углы на AB и NK равны.