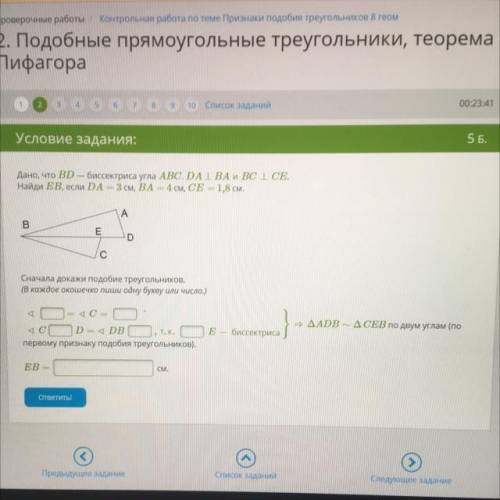
Дано, что BD – биссектриса угла ABC. DAIBA и ВС 1 СЕ. Найди EB, если DA = 3 см, ВА = 4 см, СЕ = 1,8 см.
A
B
E
D
С
Сначала докажи подобие треугольников.
(В каждое окошечко пиши одну букву или число.)
С4С-
) = 4C = (
D = 4 DB
E
первому признаку подобия треугольников).
Р
}
- ДАDB ~ ACEB по двум углам (по
Т. К.
биссектриса
ЕВ
СМ.

Дано, что BD – биссектриса угла ABC. Мы помним, что биссектриса делит угол на две равные части. Обозначим точку пересечения биссектрисы BD с линией AE как точку F.

Чтобы найти EB, нам нужно использовать знание о подобии треугольников.

Для начала, обратим внимание на треугольник ADB и треугольник CEB. Мы видим, что у них есть 2 пары равных углов:

∠DAB = ∠CEB (внутренние углы на конце стороны)
∠ABD = ∠EBC (описанные углы по биссектрисе)

Эти две пары углов делают треугольники ADB и CEB подобными по первому признаку подобия треугольников.

Также, мы знаем, что DA = 3 см, ВА = 4 см и СЕ = 1,8 см.

Теперь, обратим внимание на треугольник AFB. Мы видим, что у него есть 2 пары равных углов:

∠FAE = ∠FBA (внутренние углы на конце стороны)
∠EAF = ∠EBF (углы, составляющие прямую)

Эти две пары углов делают треугольники AEB и AFB подобными по первому признаку подобия треугольников.

Теперь мы можем записать пропорцию, используя отношения сторон подобных треугольников:

DA/AE = DB/EB

Подставляем известные значения:

3/4 = DB/EB

Чтобы найти EB, мы можем использовать простую алгебру.

Перемножаем оба числителя и оба знаменателя:

3 * EB = 4 * DB

3EB = 4DB

Теперь, чтобы избавиться от коэффициента перед EB, делим обе части уравнения на 3:

EB = (4/3) * DB

Мы хотим найти EB, но у нас дана только длина DA, а не DB. Однако, мы можем воспользоваться фактом о том, что DA + DB = BA.

Используя это уравнение, мы можем выразить DB через DA и BA:

DB = BA - DA

DB = 4 - 3

DB = 1

Теперь, зная значение DB, мы можем найти EB:

EB = (4/3) * DB

EB = (4/3) * 1

EB = 4/3

Ответ: EB = 4/3 см