Дано:
ABCD — параллелограмм,
BC= 2 см, BA= 11 см,
∡ B равен 45°.
Найти: площадь треугольника S(ABC) и площадь параллелограмма S(ABCD).
SΔABC= 2–√ см∧2;
S(ABCD)= 2–√ см параллелограмм,BC= 2 см, BA= 11 см, ∡ B равен 45°.Найти: площадь треугольн">
Другие вопросы по теме Геометрия
Популярные вопросы
- Вкаком примере выделенное слово не является эпитетом? выпишите...
3 - +my mum bought some milk ? - wh - wh - tag - a -...
3 - Как называли людей, поклоняющимся различным богам природы...
3 - Вставить н или нн? чугу…ая, ветре…ый, багря…ые, гуси…ые, маши…ое,...
2 - Вы учавствуете в забеге. вы обогнали бегуна, который занимает...
1 - 1)на какой территории была распространена католическая культура...
3 - Машина едит со скоростью 70 км ч за какое время машина проедит...
1 - 1. найдите ряд слов, в котором оба слова содержат безударную проверяемую...
2 - Прочитайте тексты и установите соответствие между текстами и их...
1 - 50 ! вставьте вместо пропусков а)в 15 веке крестьяне платили не...
1
Объяснение:
Дано:
ABCD — параллелограмм,
BC= 2 см, BA= 11 см,
∡ B = 45°.
Найти: площадь треугольника S(ABC) и площадь параллелограмма S(ABCD).
S(ABC) = 0,5*ВС*ВА*sin45° = 0,5*2*11* = см²
Диагональ делит параллелограмм на два равных треугольника, поэтому S(АВСД) = S(АВС)
S(ABCD)= 2*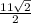 = 11
= 11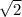 см²
см²