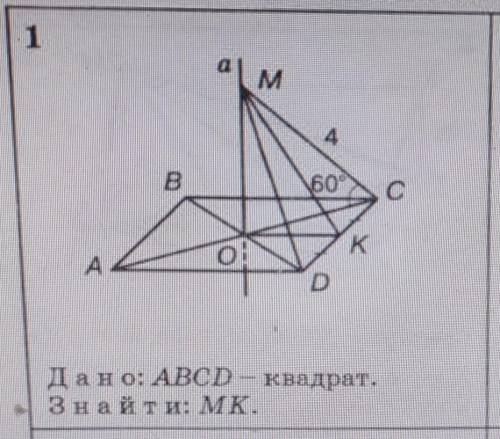
Дано: ABCD – квадрат. Знайти: МК.

Добрый день!

Для решения данной задачи, нам нужно найти длину отрезка МК.

Для начала, давайте обратимся к свойствам квадрата. В квадрате все стороны равны между собой, а углы прямые.

Нам даны точки А, В, С и D, задающие углы квадрата. Это позволяет нам легко определить длину сторон квадрата, используя расстояние между точками.

Пусть сторона квадрата равна L. Тогда:

AB = L,
BC = L,
CD = L,
DA = L.

Теперь мы можем продолжить и найти длину отрезка МК. Для этого нам понадобится теорема Пифагора.

Рассмотрим треугольник ABC. Известно, что он прямоугольный, так как все углы квадрата прямые. Поэтому можем применить теорему Пифагора:

AC^2 = AB^2 + BC^2.

AC – это диагональ, которая проходит через центр квадрата. Мы ищем МК, поэтому AC является гипотенузой, а MK – одним из катетов.

Так что мы можем переписать теорему Пифагора следующим образом:

MK^2 = AC^2 - CK^2.

Теперь давайте найдем длину диагонали AC. Обратимся к треугольнику ADC:

AD = CD = L (так как это сторона квадрата),
AC = √(AD^2 + CD^2) = √(L^2 + L^2) = √2L.

Подставляем значение AC в уравнение для MK:

MK^2 = (√2L)^2 - CK^2,
MK^2 = 2L^2 - CK^2.

Нам нужно найти MK, поэтому возьмем квадратный корень от обеих сторон уравнения:

MK = √(2L^2 - CK^2).

Теперь мы можем найти значение MK. Осталось только вычислить длину отрезка CK.

Обратимся к треугольнику BCK. У него две стороны равны L, так как это стороны квадрата, поэтому он является равнобедренным треугольником. Так как у равнобедренного треугольника два равных угла, длина высоты, проведенной из вершины угла, будет делить основание пополам.

Таким образом, CK = BC/2 = L/2.

Подставим это значение обратно в уравнение для MK:

MK = √(2L^2 - (L/2)^2),
MK = √(2L^2 - L^2/4).

Мы получили окончательное выражение для длины отрезка MK.

Чтобы получить конкретный числовой ответ, нужно знать, какое значение имеет сторона квадрата. Если мы знаем L, мы можем вставить это значение в уравнение и вычислить длину отрезка MK.

Надеюсь, я смог разъяснить эту задачу и помочь Вам понять, как решить ее. Если у Вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их!