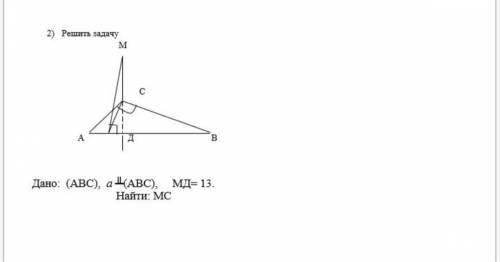
Дано: (ABC), a перпендикулярна (ABC), МД=13.
Найти: MC

Для решения этой задачи, нам нужно использовать свойства перпендикулярных прямых и теорему Пифагора.

Для начала, давайте обратим внимание на то, что прямая a перпендикулярна стороне AB треугольника ABC. Это означает, что угол MAB прямой (равен 90 градусам).

Теперь, мы можем использовать теорему Пифагора для нахождения значения MC. Вспомним, что теорема Пифагора гласит: квадрат гипотенузы (в данном случае стороны AC) равен сумме квадратов катетов (сторона AB и сторона BC).

Таким образом, у нас есть следующее уравнение:

AC^2 = AB^2 + BC^2

Так как нам дано, что сторона AB равна 13 (МД = 13), мы можем написать:

AC^2 = 13^2 + BC^2

Теперь нам нужно найти длину стороны BC. Нам дано, что прямая a перпендикулярна стороне AB. Это означает, что угол CBA также является прямым углом (90 градусов). Кроме того, нам дано, что треугольник ABC является прямоугольным (AB перпендикулярна AC). Значит, угол ACB также является прямым углом (90 градусов).

Таким образом, у нас есть два прямых угла в треугольнике ABC (CBA и ACB), что делает его прямоугольным треугольником. Так как у нас есть две прямых стороны (AB и AC), третья сторона (BC) также должна быть прямой, и длина стороны BC может быть найдена по применению теоремы Пифагора:

BC^2 = AC^2 - AB^2
BC^2 = AC^2 - 13^2

Теперь, чтобы найти длину стороны BC, нам нужно знать длину стороны AC. К сожалению, эта информация нам не дана в задаче. Если бы нам было дано значение стороны AC, мы могли бы использовать его для решения задачи. Без этой информации, задача не может быть решена.

Если у вас есть дополнительная информация или второй вариант этой задачи, я с удовольствием помогу вам решить ее!