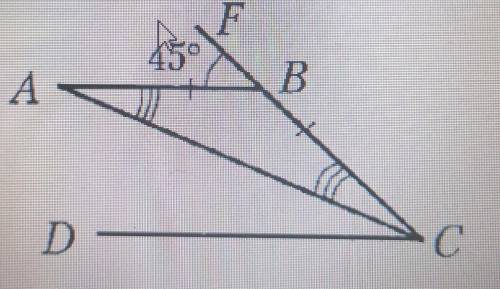
Дано;AB||CD, AB=BC, угол ABF=45°
Найти:угол лаю много

Дано, что AB || CD, AB = BC, и угол ABF = 45°.

Чтобы найти угол "лаю много" (обозначим его как ABD), нужно использовать знания о соответствующих углах, образовавшихся при пересечении параллельных прямых.

1. Из параллельности прямых AB и CD следует, что угол ABF = угол BCD (они являются соответствующими).
2. Из равенства AB = BC следует, что треугольник ABC является равнобедренным, так как две его стороны (AB и BC) равны. У равнобедренного треугольника два равных угла, называемых углами при основании.
Поэтому угол ABC = угол BAC.
3. Так как сумма углов треугольника равна 180°, мы можем вычислить угол в вершине C:
угол C = 180° - угол ABC - угол BAC.
4. Теперь мы знаем угол C, а также угол ABF (который равен 45°), поэтому можем вычислить угол BCD:
угол BCD = угол ABF - угол C.

Таким образом, мы получим значение угла "лаю много" (ABD), вычислив угол BCD по шагам, описанным выше.

Можно использовать градусомер или распечатанную геометрическую сетку для точного измерения углов и сторон на изображении.