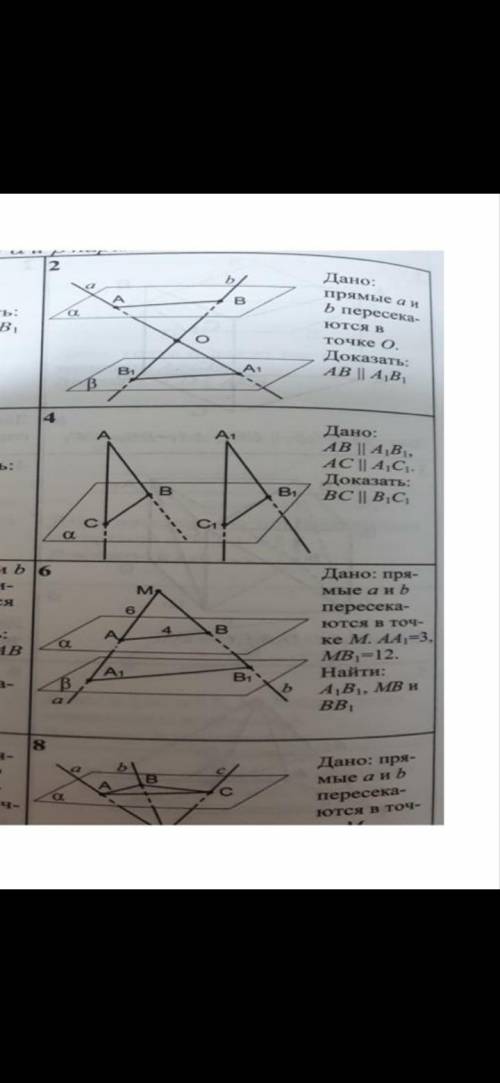
Дано ab|| a1b1 ac ||a1c1 доказать bc||b1c1

Для решения данной задачи, нам понадобятся знания о параллельных прямых и свойствах углов.

Из условия задачи мы знаем, что ab || a1b1 и ac || a1c1. Мы должны доказать, что bc || b1c1.

Для начала, давайте рассмотрим угол bac. Поскольку ab || a1b1, угол bac и угол ba1c1 - соответственные углы. Это значит, что они равны друг другу: угол bac = угол ba1c1.

Теперь рассмотрим угол bca. Поскольку ac || a1c1, угол bca и угол b1ca1 - соответственные углы. Это значит, что они равны друг другу: угол bca = угол b1ca1.

Из этих двух равенств мы можем сделать следующий вывод: угол ba1c1 = угол b1ca1.

На основании теоремы о параллельных прямых, мы знаем, что если две прямые параллельны и пересекают третью, то корреспондирующие углы равны.

Исходя из этой теоремы, мы можем сделать следующий вывод: угол abc = угол a1b1c1.

Теперь мы можем рассмотреть угол bca1. Поскольку ac || a1c1, угол bca1 и угол b1c1a1 - соответственные углы. Это значит, что они равны друг другу: угол bca1 = угол b1c1a1.

Теперь мы имеем два равенства:

угол ba1c1 = угол b1ca1
угол bca1 = угол b1c1a1

На основании этих двух равенств, мы можем сделать вывод: угол abc = угол a1b1c1 = угол b1c1a1.

Исходя из этого вывода, мы можем сделать заключение, что bc || b1c1.

Таким образом, мы доказали, что bc || b1c1 на основе данных условий и свойств параллельных прямых и углов.