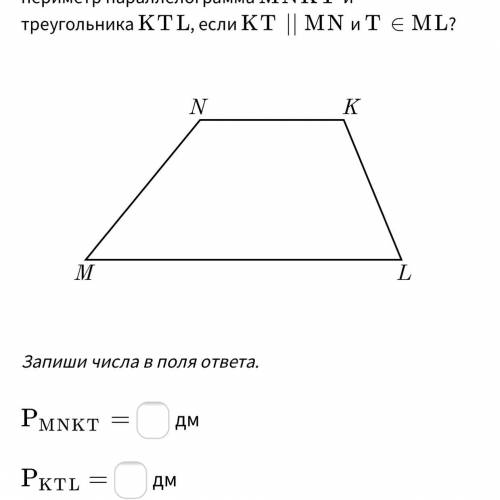
Дана трапеция  M
N
K
L
MNKL. Её основания равны 
10
10 и 
15
15 дм, а боковые стороны — 
4
4 и 
7
7 дм. Чему равен периметр параллелограмма 
M
N
K
T
MNKT и треугольника 
K
T
L
KTL, если 
K
T
∣
∣
M
N
KT∣∣MN и 
T
∈
M
L
T∈ML?

Pankl=28дм
Plus=15дм

Первым шагом нам нужно найти значение стороны KT. Мы знаем, что KT || MN, поэтому у них соответственные углы равны. Также, поскольку T принадлежит ML, угол MTN является внутренним углом трапеции MNKL.

Поскольку мы знаем значения сторон трапеции MNKL, мы можем использовать теорему Пифагора, чтобы найти значение стороны KT.

В трапеции MNKL, основания равны 10 дм и 15 дм, а боковые стороны равны 4 дм и 7 дм. Мы можем найти длину диагонали NKL, используя теорему Пифагора:

NК² = МN² + MK²
NК² = 15² + 4²
NК² = 225 + 16
NК² = 241
NК = √241
NК ≈ 15.52 дм

Теперь мы имеем значение стороны NК. Поскольку KT || MN, углы KT и NКT соответственные и равны. К тому же, угол MTN является внутренним углом трапеции. Поэтому угол KTN должен быть равен углу MTN.

Теперь мы можем использовать теорему косинусов для нахождения значения стороны KT:

KT² = NК² + НМ² – 2 * NК * NM * cos(KTN)

KT² = 15.52² + 10² – 2 * 15.52 * 10 * cos(KTN)
KT² = 240.6 + 100 – 310.4 * cos(KTN)
KT² = 340.6 – 310.4 * cos(KTN)

Теперь у нас есть значение стороны KT. Мы можем использовать это значение, чтобы найти периметр параллелограмма MNKT. Периметр параллелограмма — это сумма всех четырех его сторон.

Периметр параллелограмма MNKT = МN + NT + TK + KM.

Мы уже знаем значения сторон МN и ТК. Нам нужно найти значения сторон NT и KM.

Сначала найдем значение стороны NT, используя теорему Пифагора:

NT² = KT² + NК² – 2 * KT * NК * cos(NTK)
NT² = KT² + 15.52² – 2 * KT * 15.52 * cos(NTK)

Теперь найдем значение стороны KM, используя ту же теорему Пифагора:

KM² = MN² + NК² – 2 * MN * NК * cos(MNK)
KM² = 10² + 15.52² – 2 * 10 * 15.52 * cos(MNK)

Теперь у нас есть значения всех четырех сторон параллелограмма MNKT. Мы можем сложить их, чтобы найти его периметр.

Сумма сторон параллелограмма MNKT = МN + NT + TK + KM

Теперь, нам нужно найти периметр треугольника KTL. Для этого нам нужно сложить длины всех его сторон.

Периметр треугольника KTL = KT + KM + ML

При решении задачи, нужно использовать найденные значения сторон KT, NT и KM для подсчета периметра параллелограмма MNKT и треугольника KTL. Также, с непонятными формулами или теоремами можно обратиться за объяснением к учителю.