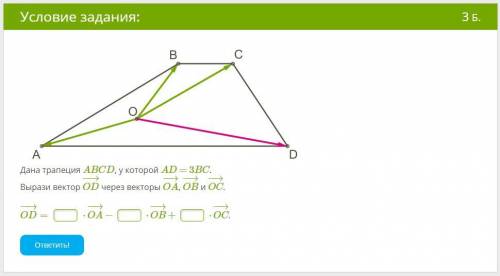
Дана трапеция ABCD, у которой AD = 3BC.
Вырази вектор OD−→− через векторы OA−→−, OB−→− и OC−→−

Для начала, необходимо определить, что такое вектор. Вектор - это математический объект, который характеризуется не только длиной, но и направлением и начальной точкой. В данной задаче, вектор обозначается стрелкой над названием буквы, например, OA-> - это вектор, идущий от начальной точки O и указывающий на точку A.

Теперь рассмотрим данную трапецию ABCD. У нас дано, что AD = 3BC. Используя данный факт, мы можем привести BC к виду AD, умножив его на 3. То есть, BC = (1/3)AD.

Следующим шагом нам необходимо выразить вектор OD-> через векторы OA->, OB-> и OC->. Заметим, что вектор OD-> можно представить как сумму векторов OA->, OB-> и BC->. Поскольку BC-> равняется (1/3)AD->, мы можем переписать это в виде: OD-> = OA-> + OB-> + (1/3)AD->.

Теперь нам нужно выразить AD-> через OA->, OB-> и OC->. Заметим, что AD-> можно разделить на две части: AD-> = AC-> + CD->. Но мы пока не знаем значения векторов AC-> и CD->.

Чтобы выразить AC-> и CD-> через OA->, OB-> и OC->, мы можем воспользоваться свойствами параллелограмма. Данный задан так, что AB и CD - параллельные прямые, а значит, векторы AB-> и CD-> равны друг другу. То есть, AB-> = CD->.

Т.к. ABCD - параллелограмм, мы также можем сказать, что AC-> = OB->, поскольку AC и OB - параллельные прямые и имеют равные длины.

Используя эти факты, мы можем выразить CD-> через OA->, OB-> и OC->. CD-> = AB-> = OA-> - OB->.

Теперь у нас есть выражения для AC-> и CD->: AC-> = OB-> и CD-> = OA-> - OB->.

Подставив эти значения в выражение AD-> = AC-> + CD->, получим AD-> = OB-> + (OA-> - OB->), что можно упростить до AD-> = OA->.

Теперь мы знаем, что AD-> равно OA->, значит, OD-> можно представить следующим образом: OD-> = OA-> + OB-> + (1/3)AD->.

Подставим значение AD-> = OA-> в эту формулу: OD-> = OA-> + OB-> + (1/3)OA->.

Упрощаем выражение: OD-> = 4/3 OA-> + OB->.

Итак, мы получили выражение для вектора OD-> через векторы OA->, OB-> и OC->: OD-> = 4/3 OA-> + OB->.