Дан параллелограмм ABCD известно что А (2;5; - 1)В (- 5;4 ;- 4)c (1 - 2;2) найдите а) координаты точки пересечения диагоналей, б) длину AB , в) координаты вершины D

Объяснение:

Раз нам даны точки в пространстве, то скорее всего с векторами уже знакомы, тогда. Найдем векторы АВ и ВС, для этого нужно от координат конца отнять соответствующие координаты начала, тогда

(в)АВ(-5-2;4-5;-4-(-1))=(-7;-1;-3)

(в)BC(1-(-5);-2-4;2-(-4))=(6,-6,6)

По определению параллелограма это четырехугольник у которого 2 пары параллельных равных сторон, сделовательно (в)AB=(в)CD

(в)AB(-7;-1;-3), C(1;-2;2) Пусть точка D имеет координаты x,y,z. Следовательно (в)CD(x-1;y+2;z-2) и эти выражения x-1;y+2;z-2 соответственно равны -7;-1;-3. Тогда

x-1=-7⇔x=-6

y+2=-1⇔y=-3

z-2=-3⇔z=-1. Следовательно координаты точки D(-6,-3,-1)

Так как диагональ точкой пересечения делится пополам, то точка пересечения диагоналей это середина диагонали, диагональ - отрезок соединяющий 2 несоседние вершины, значит найдем середину BD или АС

Координаты середины отрезка находятся по формуле среднего арифмитеческого соответствующих координат концов, т.е. абсцисса первой точки+ абсцисса второй точки делить на 2, ордината и апликата соответственно, тогда

Середина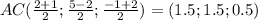 Точка с этими координатами,пусть точка О, и есть точка пересечения диагоналей.

Длина AB .длина вектора это есть квадратный корень из суммы квадратов его координат, тогда длина АВ = длине вектора АВ

|(в)АВ|=