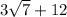Четырёх угольник авсд вписан в окружность радиуса 8. известно ав=вс=сд=12. доказать. что вс и ад параллельны. найти ад. указание. возможно понадобится найти синус 3х. его можно найти через сумму синусов х и 2х.
Другие вопросы по теме Геометрия
Популярные вопросы
- Task 3. Write the questions in the past and answer them Example: 0) Did they live...
2 - Task1. Read the short texts about fantasy creatures. There are lots of stories...
1 - У томата рассеченный лист доминантен по отношению к цельному. При скрещиванти...
1 - Укажите предложение, содержащее вводное ПРЕДЛОЖЕНИЕ которое следует выделить запятыми...
1 - 1. Решите уравнение: 9,4 - (1,6 – 4y)= - 11,8 дам 2задание решите уравнение 6|х-7|=144...
1 - Найти значение выражения.а...
2 - Сравнительная характеристика Римского-корсакова и Чайковского? Чем больше тем...
1 - хлопчик розтягує гумовий шнур прикладаючи силу 100 H.визначте жорсткість гуми...
3 - Источники о саксах можно найти в трудах греко-римских авторов. Саклар - древнее...
1 - 5.Изобразите на координатной прямой и запишите пересечение и объединениечисловых...
3
1) Т.к. углы CDB и CAB опираются на одну и ту же дугу, то они равны. Тогда треугольники DCB и ABC равны по стороне и 2-м углам(AC общая, а углы CDB=DBC=CAB=BAC т.к. треугольники DCB и ABC равнобедренные и углы CDB=CAB см. выше). Треугольники DCA и ABD равны по тому же принципу. В итоге треугольники CTB и DTA равнобедренные, а т.к. углы CTB и DTA вертикальные, то углы TDA и TBC равны, а это признак параллельности прямых, тогда CB || AD.
2) Пусть ACB=α. По формуле радиуса описанной окружности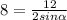 , тогда
, тогда  . Угол DCA=180-3α. По теореме синусов имеем
. Угол DCA=180-3α. По теореме синусов имеем 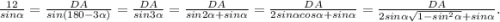 . Теперь подставляем значение sinα=3/4 и вычисляем. У меня получилось
. Теперь подставляем значение sinα=3/4 и вычисляем. У меня получилось