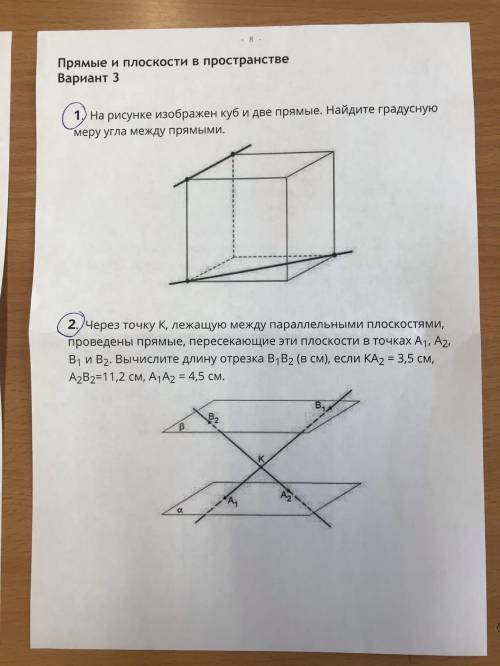
Через точку K, лежащую между параллельными плоскостями, проведены прямые, пересекающие эти плоскости в точках А1, А2, В1 и В2. Вычислите длину отрезка В1В2 (в см) если КА2=3,5см, А2В2=11,2 см, А1А2=4,5см

Чтобы решить эту задачу, мы можем использовать теорему Талеса, которая гласит: "Если параллельные прямые пересекаются прямой, проведенной через одну из них, то соответствующие сегменты на одной из пересекающихся прямых пропорциональны".

Исходя из данной теоремы, мы можем установить пропорцию:

AB1/AK = AB2/AK

Теперь мы можем использовать известные значения для решения этой пропорции. Из условия задачи у нас есть следующая информация:

AK = KA2 + A2B2 = 3.5 см + 11.2 см = 14.7 см

А также длина отрезка А1А2, которую мы обозначим как x: А1А2 = x = 4.5 см

Мы можем записать пропорцию следующим образом:

AB1/14.7 см = AB2/14.7 см + 4.5 см

Теперь нам нужно найти длину отрезка В1В2, которую мы обозначим как y.

Зная пропорцию, мы можем записать следующее:

y/14.7 см = 14.7 см + 4.5 см/14.7 см

Теперь мы можем решить эту пропорцию:

y = (14.7 см + 4.5 см) * 14.7 см

y = 19.2 см * 14.7 см

y = 282.24 см²

Таким образом, длина отрезка В1В2 равна 282.24 см.