1. Геометрия
  2. буду очень благодарен

буду очень благодарен очень надо (геометрия) ответ расписать ​всё з 7 по 9


буду очень благодарен очень надо (геометрия) ответ расписать ​всё з 7 по 9

leonde leonde    1   08.04.2021 19:45    0

Ответы
Xadice12345 Xadice12345  08.05.2021 19:50
7.

Формула вычисления стороны квадрата, зная описанный радиус: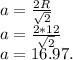 a = \frac{2R}{\sqrt{2}}\\a = \frac{2*12}{\sqrt2}\\a = 16.97.

Формула вычисления радиуса вписанной окружности в квадрат, зная его сторону:

a = 2r\\16.97 = 2r \Rightarrow r = 16.97/2 = 8.5.

Вывод: Сторона квадрата равна: 16.97; радиус вписанной окружности — 8.5.

8.

Формула вычисления радиуса описанной окружности, зная сторону правильного треугольника:

R = \frac{a}{\sqrt3}\\R = \frac{10}{\sqrt3}\\R = 5.8.

Длина круга равна:

L = 2\pi R\\L = 2\pi 5.8\\L = 36.44.

Не поняла, площадь какого круга надо найти, так что найду площади и вписанной, и описанной окружности.

Формула вычисления площади описанной окружности такова:

S = \pi*R^2\\S = /pi*5.8^2\\S = 105.7^2.

Формула вычисления площади вписанной окружности такова: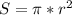 S = \pi*r^2

Радиус вписанной окружности в правильный треугольник, мы найдём по стороне этого же треугольника:

r = \frac{a}{2\sqrt{3}}\\r = \frac{10}{2\sqrt{3}}\\r = 2.85.

Площадь окружности равна:

S = \pi*2.85^2\\S = \pi*8.12\\S = 25.51^2.

9.

Формула вычисления стороны правильного треугольника, зная радиус описанной окружности:

\displaystyle\\R = \frac{a}{\sqrt3}\\\\6\sqrt{3} = \frac{a}{\sqrt3}\\\\a = 6\sqrt{3}*\sqrt3\\a = 17.9.

Радиус вписанной окружности равен:

r = \frac{a}{2\sqrt{3}}\\r = \frac{10.9}{2\sqrt{3}}\\r = 3.114.

Площадь окружности равна:

S = \pi * r^2\\S = \pi*3.114^2\\S = 30.5^2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
llleeennn llleeennn  03.06.2020 22:37
это очень Два номера. заранее благодарю это очень Два номера. заранее благодарю >...
olesiadukova olesiadukova  03.06.2020 22:34
Выбери верное утверждение. В ответе укажи его номер. 1. Существует вписанный четырёхугольнике, сумма противоположных углов в котором равна 120 градусов. 2. Если вписанный...
олжас200 олжас200  03.06.2020 22:28
Площадь трапеции, изображённой на рисунке, равна 528, основание b=23, высота h=22. Найди второе основание трапеции....
ПочтиОтличникМакс ПочтиОтличникМакс  03.06.2020 10:27
Найти площадь, ограниченную параболой y = 4x – x2 и прямой у = х+2. С рисунком...
TAMADA123123 TAMADA123123  29.09.2019 08:30
При пересечении двух прямых образовались четыре угла один из которых равен 110 градусов найдите остальные углы...
LaMihaLa LaMihaLa  29.09.2019 08:30
Прямые ac и bd не лежат в одной плоскости. докажите, что прямые ab и cd не лежат в одной плоскости. заранее )...
grafPypirkin grafPypirkin  29.09.2019 08:30
Как на плоскости расположены точки a,h,e,если ae=eh=ha...
vikavikt vikavikt  29.09.2019 08:30
1.знайдіть гострий кут між діагоналями прямокутника якщо його діагональ утворює зі стороною кут 35* . 2.знайдіть периметр ромба якщо його сторона утворює з діагоналлю...
Liya20034 Liya20034  29.09.2019 08:30
Сколько спиц в колесе, если угол между соседними спицами равен 20°...
kira315 kira315  29.09.2019 08:40
Найдите градучные величины двух смежных углов если один из низ в два раза больше другого...

Популярные вопросы