Найти площадь, ограниченную параболой y = 4x – x2 и прямой у = х+2. С рисунком
Другие вопросы по теме Геометрия
Популярные вопросы
- №4 Complete the sentences.Use Present Simple, Present Continuous,...
1 - До е геометричним мисцем толчок ривновидалених вид сторон кута...
1 - Колебательный контур. Формула Томсона. 1) Как изменятся период и...
3 - Физика. Заранее за 5 небольших задач. ...
2 - А) Опишите государственное устройство США: форма правления, президент,...
3 - НУЖЕН ОТВЕТ Привлекая обществоведческие знания, составьте краткое...
2 - Электрон движется в однородном магнитном поле с индукцией 10 мТл....
3 - Период творчества А. Пушкина, в который было создано произведение...
3 - Нужно разложить на множители. -6x^2+7x-2...
3 - 2. Чи були у героїв твору Всеволода Нестайка прототипи? 1. так,...
3
Приравняем данные функции и решим полученное квадратное уравнение:
По формуле Ньютона-Лейбница найдём площадь:
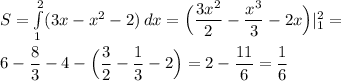
ответ: