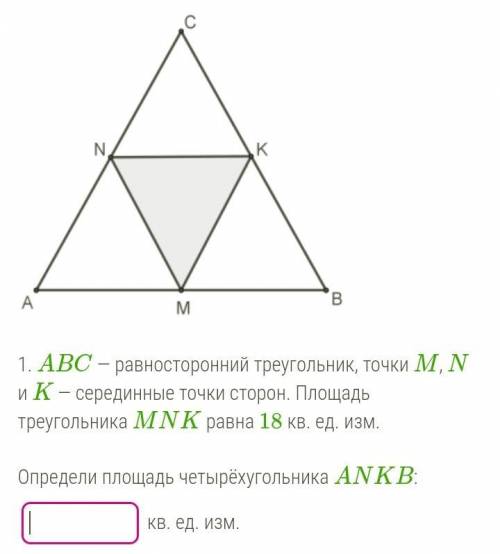
ABC — равносторонний треугольник, точки M, N и K — серединные точки сторон. Площадь треугольника MNK равна 18 кв. ед. изм. Определи площадь четырёхугольника ANKB

Для решения данной задачи нужно использовать свойства равностороннего треугольника и знание формулы площади треугольника.

Поскольку треугольник ABC является равносторонним, то все его стороны равны между собой. Обозначим длину стороны треугольника ABC как а.

Также, по определению серединной точки стороны треугольника, точка M является серединной точкой стороны AB. Значит, отрезок AM является половиной стороны AB, то есть его длина равна a/2.

Аналогично, точка N является серединной точкой стороны BC, и отрезок BN имеет длину a/2.

Также точка K является серединной точкой стороны AC, и длина отрезка AK также составляет a/2.

Теперь рассмотрим треугольник MNK. Этот треугольник получается из треугольника ABC путем удаления треугольников AMK, BMN и CNK. Каждый из этих треугольников имеет площадь, равную 1/4 от площади треугольника ABC. Поскольку треугольник MNK получается путем удаления этих трех треугольников, то его площадь равна:
S(MNK) = S(ABC) - 3*S(AMK) = (a^2 * sqrt(3))/4 - 3*(a/2 * a/2 * sqrt(3))/4 = (a^2 * sqrt(3))/4 - (3 * a^2 * sqrt(3))/16 = (a^2 * sqrt(3))/4 - (3 * a^2 * sqrt(3))/16 = (4 * a^2 * sqrt(3))/16 - (3 * a^2 * sqrt(3))/16 = a^2 * sqrt(3)/16.

Из условия задачи известно, что площадь треугольника MNK равна 18 кв.ед. Запишем это условие в виде уравнения и решим его для определения значения а:

a^2 * sqrt(3)/16 = 18.

Умножим обе части уравнения на 16 и разделим на sqrt(3):

a^2 = 288/sqrt(3).

Возведем обе части уравнения в квадрат, чтобы избавиться от корня:

a = sqrt(288/sqrt(3)).

Теперь, когда мы знаем значение длины стороны треугольника ABC, мы можем найти площадь четырехугольника ANKB. Для этого разобьем его на два треугольника: ANK и NKB, и найдем площадь каждого из них.

Площадь треугольника ANK равна половине площади треугольника ABC. Известно, что площадь треугольника ABC составляет a^2 * sqrt(3)/4, поэтому площадь треугольника ANK равна (1/2)(a^2 * sqrt(3)/4) = a^2 * sqrt(3)/8.

Аналогично, площадь треугольника NKB также равна половине площади треугольника ABC, то есть a^2 * sqrt(3)/8.

Площадь четырехугольника ANKB равна сумме площадей треугольников ANK и NKB:

S(ANKB) = S(ANK) + S(NKB) = a^2 * sqrt(3)/8 + a^2 * sqrt(3)/8 = (2a^2 * sqrt(3))/8 = a^2 * sqrt(3)/4.

Таким образом, площадь четырехугольника ANKB равна a^2 * sqrt(3)/4.

В ответе можно подставить значения a (которое мы нашли ранее) и рассчитать конечный числовой ответ.