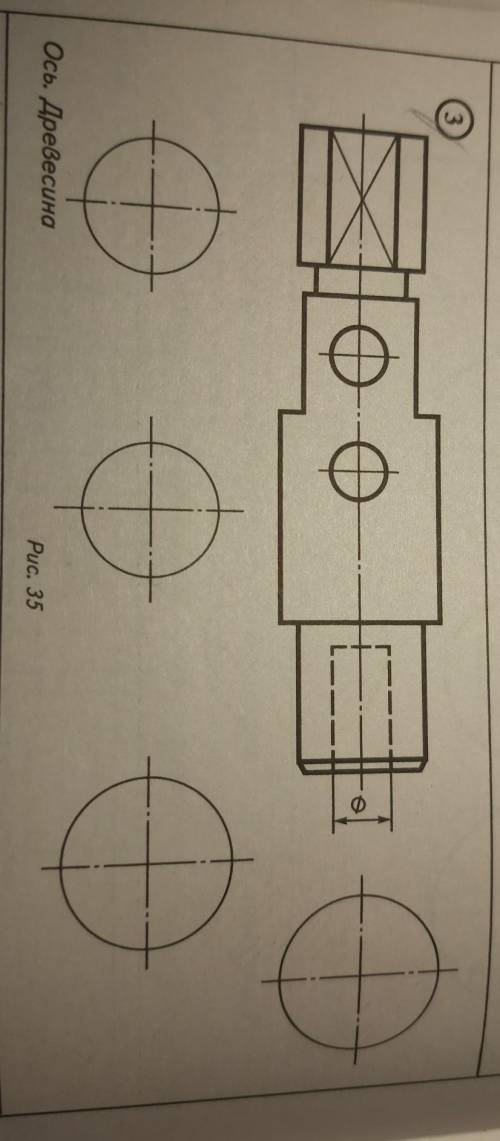
16. Проанализировать геометрическую форму точеной дета- ли, определить рациональные сечения, построить их и
обозначить (рис. 33—36). На полках линий-выносок ука-
зать названия конструктивных элементов детали.​

16. Для анализа геометрической формы данной точеной детали и определения рациональных сечений, нам потребуется аккуратно рассмотреть ее изображение на рисунке.

Сначала посмотрим на саму деталь. Она состоит из двух основных частей: цилиндрической части и конической части. Цилиндрическая часть имеет постоянный радиус и высоту, а коническая часть имеет угол наклона и меняющийся радиус от вершины конуса к цилиндрической части.

Чтобы определить рациональные сечения, рассмотрим различные пересечения плоскостей с деталью.

Рациональные сечения - это такие плоскости, которые пересекают деталь таким образом, что получаются геометрически простые фигуры, такие как круги или прямоугольники. Они легко определяются и могут быть использованы для упрощения анализа и конструирования детали.

На рисунке даны 4 возможных рациональных сечения, обозначенные как A, B, C и D. Давайте подробнее рассмотрим каждое из них:

Сечение A:
Это горизонтальное сечение, которое проходит через цилиндрическую часть детали. Оно является кругом с постоянным радиусом, равным радиусу цилиндрической части детали. Такое сечение будет полезно для измерения диметра детали и ее высоты.

Сечение B:
Это вертикальное сечение, которое проходит через центр конусной части детали. Оно также является кругом, но его радиус будет меняться от вершины конуса к основанию. Такое сечение покажет нам форму конусной части детали.

Сечение C:
Это вертикальное сечение, которое проходит вблизи основания конусной части детали. Такое сечение будет прямоугольником, так как его форму можно считать прямолинейной. Оно поможет нам определить размеры и положение основания конусной части.

Сечение D:
Это горизонтальное сечение, которое проходит вблизи вершины конуса. В этом случае, сечение будет представлять собой эллипс. Этом сечение позволит нам увидеть форму вершины конусной части.

Теперь, когда мы проанализировали 4 рациональных сечения и их геометрическую форму, давайте построим их на рисунке:

1. Для сечения A (цилиндрическая часть), нарисуем круг радиусом, равным радиусу цилиндрической части детали.
2. Для сечения B (вертикальное сечение через центр конуса), нарисуем круг с изменяющимся радиусом от вершины конуса до основания.
3. Для сечения C (вертикальное сечение вблизи основания конуса), нарисуем прямоугольник с размерами, соответствующими основанию конусной части.
4. Для сечения D (горизонтальное сечение вблизи вершины конуса), нарисуем эллипс, соответствующий форме вершины конусной части.

Таким образом, построив все 4 рациональных сечения на рисунке, мы сможем лучше понять геометрическую форму данной точеной детали и ее конструктивные элементы.

На полке линий-выносок, мы можем указать названия конструктивных элементов детали:

1. Цилиндрическая часть - это основная часть детали, имеющая круглую форму с постоянным радиусом.
2. Коническая часть - это вторая часть детали, имеющая форму конуса с изменяющимся радиусом и углом наклона.
3. Основание конуса - это самая широкая часть конуса, которая имеет форму круглого сечения и позволяет детали стабилизироваться.
4. Вершина конуса - это самая узкая часть конуса, которая также является самой острым углом наклона.

Таким образом, проведя анализ геометрической формы данной точеной детали и определив рациональные сечения, построив их и обозначив конструктивные элементы, мы сможем получить полное представление о форме и структуре этой детали. Более того, такой анализ поможет нам лучше понять ее свойства и использовать эту информацию при ее дальнейшем конструировании и использовании.