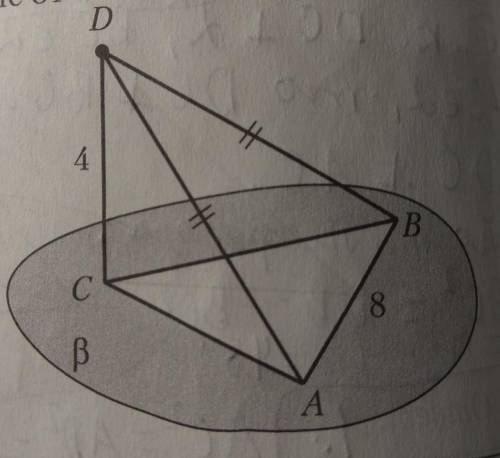
Дано: DC перпендикулярно бета, DC=4, AD=BD, AB=8, Pabc=18. Найти: расстояние от точки D до прямой AB.
Другие вопросы по теме Геометрия
Популярные вопросы
- Составить вопросительное предложение с местоимениями 2 лица ед.ч....
2 - Колебательный контур состоит из катушки индуктивностью l=2,0...
1 - Утрьох вагонах 840 т вугілля. скільки т вугілля в кожному вагоні...
1 - Из двух городов, расстояние между которыми 20 км, одновременно...
2 - Сязыком надо описать двух моделей jake and robert....
2 - Напишити текст по общение с прадовцом...
3 - Напешите как вы понимаете смысл пословицы кто рано встал тот...
3 - Написать анализ стихотворения н. а. заболоцкого я не ищу гармонии...
2 - Сумма двух углов равнобедренной трапеции равна 336 градусов ....
1 - Синдикаторной бумажки определите, в какой из выданных вам пробирок...
3
Обратим внимание, что в треугольнике DBC стороны DB и DC являются равными, так как дано AD = BD и DC = 4. Также известно, что угол BDC прямой (так как DC перпендикулярно β).
Теперь рассмотрим треугольник ABC. Мы знаем, что стороны AB и BC равны 8 и 4 соответственно.
Перейдем к такому подходу: построим высоту DE из точки D на сторону AC. Поскольку угол BDC прямой, то треугольник BDE также прямоугольный.
Задача сводится к нахождению длины отрезка DE.
Обозначим неизвестную длину DE как х.
В прямоугольном треугольнике BDE по теореме Пифагора имеем:
BD^2 = BE^2 + DE^2 (*)
Так как AD = BD и DC = 4, то AC = 8 - 4 = 4.
Далее воспользуемся теоремой Пифагора и применим ее к треугольнику ABC:
AC^2 = AB^2 - BC^2
4^2 = 8^2 - 4^2
16 = 64 - 16
16 = 48
Итак, получили значение AC^2 = 48.
Зная значение AC^2, можем выразить значение BE:
BE = (√(AC^2 - DE^2 (из (*) )) = (√(48 - х^2))
Теперь можем подставить значение BE в уравнение (*), получим:
BD^2 = (√(48 - х^2))^2 + х^2
CB^2/9 = 48 - х^2 + х^2
CB^2/9 = 48
Получили уравнение: CB^2/9 = 48
Разделим обе части уравнения на 48 и умножим на 9:
CB^2 = 48 * 9
CB^2 = 432
Теперь извлечем квадратный корень из обеих сторон уравнения:
CB = √432
Разложим 432 на простые множители:
432 = 2 * 2 * 2 * 2 * 3 * 3 * 3
CB = √(2^4 * 3^3)
CB = (2^2 * 3) * √3
CB = 6√3
Теперь мы знаем длину стороны CB, которая равна 6√3.
Нам осталось найти длину отрезка DE.
Из уравнения (*), BD^2 = BE^2 + DE^2, получаем:
4^2 = (√(48 - х^2))^2 + х^2
16 = 48 - х^2 + х^2
Сокращаем одинаковые слагаемые и получаем:
16 = 48
Получили ложное уравнение, из чего делаем вывод, что такого значения х не существует.
То есть, отрезок DE не существует и высота DE опущена из точки D на сторону AC треугольника ABC.
Итак, расстояние от точки D до прямой AB равно длине стороны CB, то есть 6√3.