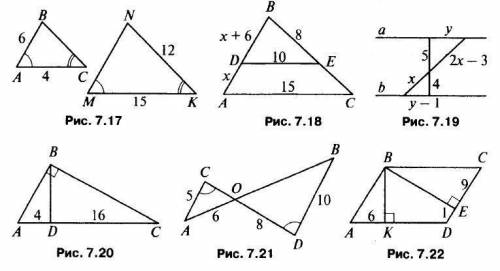
1. Рис. 7.17. Найти: ВС, MN. 2. Дано: DE||АС (рис. 7.18). Найти: АВ, ВС.
3. Дано: а||b (рис. 7.19). Найти: х, у.
4. Рис. 7.20. Найти: BD.
5. Рис. 7.21. Найти: СО, ВО.
6. Рис. 7.22. Найти: ВС.
Задачи решаются с использованием «Первого признака подобия» двух треугольников. Дано можно записать кратко. Чертежи к каждой задаче нужно перенести в тетрадь.
Другие вопросы по теме Геометрия
Популярные вопросы
- Сочинение на тему наступила золотая осень деревья оделись в разноцветные...
3 - Відредагувати текст: ми з сергієм завжди приймаємо активну участь...
3 - Уменя самостоятельная ! 1)в каком формате нужно сохранить файл чтобы...
1 - Какая здесь основная тема? в чем заключается основная мысль? в конце...
1 - Ежедневно на базу привозят 30 т капусты, а увозят в магазины 500...
2 - Сумарная солнечная радиация в москве, санк-петербурге, мурманске?...
3 - Звуко буквенный разбор слова усатый...
1 - Мама дола маше 35 рублей . маша пошла чтоб купить унику и тетрадь...
3 - Сравнить сказки спящая царевна и сказка о мертвой царевне...
3 - Разбавленная серная кислота напишите уравнения реакций а)разбавленной...
3
Шаг 1: Посмотрим на треугольник АВС и треугольник АMN. Сравним соответствующие стороны треугольников. ВС соответствует MN.
Шаг 2: Если стороны треугольников пропорциональны, то треугольники подобны. Так как ВС соответствует MN, то треугольники АВС и АMN подобны.
Шаг 3: Используя свойство подобных треугольников, можно записать пропорцию:
AB/AM = AC/AN
Шаг 4: Найдем значения AB и AC из данных в задаче и подставим их в пропорцию:
AB/AM = AC/AN
AB/9 = 6/2
AB = 9 * (6/2)
AB = 27
Таким образом, AB = 27.
2. Для решения второй задачи (рис. 7.18) также нужно использовать первый признак подобия треугольников. Данные в задаче: DE||АС. Нужно найти АВ и ВС.
Шаг 1: Рассмотрим треугольник АВС и треугольник АDE. Сравним соответствующие стороны треугольников. AB соответствует AD, а ВС соответствует DE.
Шаг 2: Так как АВ соответствует AD, и ВС соответствует DE, треугольники АВС и АDE подобны.
Шаг 3: Используя свойство подобных треугольников, можно записать пропорции:
AB/AD = AC/AE
VS/DE = AC/AE
Шаг 4: Найдем значения AB и DE из данных в задаче и подставим их в пропорции:
AB/AD = AC/AE
AB/10 = 8/4
AB = 10 * (8/4)
AB = 20
VS/DE = AC/AE
VS/8 = 8/4
VS = 8 * (8/4)
VS = 16
Таким образом, AB = 20 и VS = 16.
3. Для решения третьей задачи (рис. 7.19) также используется первый признак подобия треугольников. Данные в задаче: а||b. Нужно найти х и у.
Шаг 1: Рассмотрим треугольник АВС и треугольник MNQ. Сравним соответствующие стороны треугольников. AB соответствует MN, а ВС соответствует NQ.
Шаг 2: Так как AB соответствует MN, и ВС соответствует NQ, треугольники АВС и MNQ подобны.
Шаг 3: Используя свойство подобных треугольников, можно записать пропорции:
AB/MN = AC/NQ
BC/QR = AC/НE
Шаг 4: Найдем значения AB и НЕ из данных в задаче и подставим их в пропорцию:
AB/MN = AC/ NQ
AB/8 = 12/6
AB = 8 * (12/6)
AB = 16
BC/QR = AC/HE
BC/8 = 12/10
BC = 8 * (12/10)
BC = 9.6
Таким образом, AB = 16 и BC = 9.6.
4. В четвертой задаче (рис. 7.20) надо найти BD. Для этого нужно использовать первый признак подобия треугольников.
Шаг 1: Рассмотрим треугольник ABC и треугольник BDE. Сравним соответствующие стороны треугольников. AB соответствует BE, а AC соответствует BD.
Шаг 2: Так как AB соответствует BE, и AC соответствует BD, треугольники ABC и BDE подобны.
Шаг 3: Используя свойство подобных треугольников, можно записать пропорцию:
AB/BE = AC/BD
Шаг 4: Найдем значения AB и BE из данных в задаче и подставим их в пропорцию:
AB/BE = AC/BD
4/8 = 7/BD
Шаг 5: Решим пропорцию:
4/8 = 7/BD
BD = (8 * 7)/4
BD = 14
Таким образом, BD = 14.
5. В пятой задаче (рис. 7.21) нужно найти СО и ВО. Для этого также используем первый признак подобия треугольников.
Шаг 1: Рассмотрим треугольник ABC и треугольник BCD. Сравним соответствующие стороны треугольников. AB соответствует BD, а AC соответствует BC.
Шаг 2: Так как AB соответствует BD, и AC соответствует BC, треугольники ABC и BCD подобны.
Шаг 3: Используя свойство подобных треугольников, можно записать пропорции:
AB/BD = AC/BC
CO/CD = AC/BC
BO/BD = CO/CD
Шаг 4: Найдем значения AB, AC и BC из данных в задаче и подставим их в пропорцию:
AB/BD = AC/BC
3/6 = 8/BC
CO/CD = AC/BC
CO/5 = 8/BC
BO/BD = CO/CD
BO/6 = CO/5
Шаг 5: Решим пропорции:
3/6 = 8/BC
BC = (6 * 8)/3
BC = 16
CO/5 = 8/BC
CO/5 = 8/16
CO = (8 * 5)/16
CO = 2.5
BO/6 = CO/5
BO/6 = 2.5/5
BO = (6 * 2.5)/5
BO = 3
Таким образом, СО = 2.5 и ВО = 3.
6. В шестой задаче (рис. 7.22) нужно найти ВС. Для этого снова используется первый признак подобия треугольников.
Шаг 1: Рассмотрим треугольник ABC и треугольник DCE. Сравним соответствующие стороны треугольников. AB соответствует DC, а ВС соответствует DE.
Шаг 2: Так как AB соответствует DC, и ВС соответствует DE, треугольники ABC и DCE подобны.
Шаг 3: Используя свойство подобных треугольников, можно записать пропорцию:
AB/DC = AC/DE
Шаг 4: Найдем значения AB и DC из данных в задаче и подставим их в пропорцию:
AB/DC = AC/DE
9/VE = 12/CE
Menù