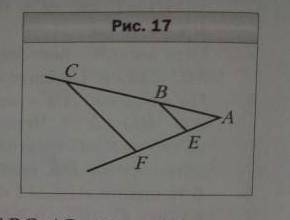
1) На рисунке 17 CF || BE, AE=6см. EF=14см, BC=35см. Найдите
отрезок Ab
2) Треугольники ABC и A1 B1 C1
подобны, причем сторонам
AC и BC соответствуют
стороны этих треугольников,
если AC=28см, AB=49см,
B1 C1 =24см, A1 C1 =16см
3) Отрезок CK- биссектриса
треугольника ABC, AC=45см,
AK=18см, BK=10см. Найдите
сторону BC
4) На стороне AB треугольника
ABC отметили точку M так,
что AM : MB=4:9. Через точку
M провели прямую, которая
паралельна стороне BC
треугольника и пересекает
сторону AC в точке K.
найдите отрезок MK, если
BC=26см.
СДЕЛАЙТЕ КОНТРОЛЬНУЮ ПО ГЕОМЕТРИИ.
Ответы
1) В данном случае мы имеем параллельные прямые CF и BE, и мы знаем значения отрезков AE, EF и BC. Наша задача - найти значение отрезка Ab.
Для решения этой задачи мы можем использовать теорему о подобии треугольников. Поскольку прямые CF и BE параллельны, то треугольники AEF и ABC подобны.
Мы можем записать пропорцию между сторонами этих двух треугольников:
AE/AB = EF/BC
Подставим известные значения в эту пропорцию:
6/Ab = 14/35
Перекрестное умножение:
14 * Ab = 6 * 35
Ab = (6 * 35)/14
Подсчитаем:
Ab = 15 см
2) В данном случае у нас есть два подобных треугольника: ABC и A1B1C1. Мы знаем значения сторон AC, BC, B1C1 и A1C1 и хотим найти значения сторон AB и B1C1.
Поскольку эти два треугольника подобны, мы можем записать пропорцию между сторонами:
AC/AB = B1C1/BC
Подставим известные значения:
28/AB = 24/49
Перекрестное умножение:
24 * AB = 28 * 49
AB = (28 * 49)/24
Подсчитаем:
AB = 57.67 см (округлить до двух десятичных знаков)
B1C1/BC = 16/24
Перекрестное умножение:
16 * BC = 24 * B1C1
BC = (24 * B1C1)/16
BC = (24 * 24)/16
Подсчитаем:
BC = 36 см
3) В данном случае у нас есть треугольник ABC и биссектриса CK. Мы знаем значения сторон AC, AK, BK и хотим найти значение стороны BC.
Мы можем использовать теорему биссектрисы, которая гласит:
AK/CK = AB/BC
Подставим известные значения:
18/CK = AB/45
Перекрестное умножение:
18 * 45 = AB * CK
AB = (18 * 45)/CK
AB = 810/CK
Также известно, что AK + BK = AB
Подставим известные значения:
18 + 10 = AB
AB = 28
Подставим это в предыдущее уравнение:
810/CK = 28
Перекрестное умножение:
28 * CK = 810
CK = 810/28
Подсчитаем:
CK = 28.93 см (округлить до двух десятичных знаков)
4) В данном случае мы имеем треугольник ABC, где на стороне AB отмечена точка M. Мы знаем отношение AM:MB и длину стороны BC. Наша задача - найти длину отрезка MK.
Поскольку прямая, проведенная через точку M, параллельна стороне BC, то по теореме Талмана (также известной как теорема подобия треугольников) мы можем записать пропорцию между сторонами треугольников ABC и AMK:
AM/MB = AK/KM
Подставим известные значения:
4/9 = 18/KM
Перекрестное умножение:
4 * KM = 18 * 9
KM = (18 * 9)/4
Подсчитаем:
KM = 40.5 см
Ответы:
1) Отрезок Ab = 15 см
2) AB = 57.67 см, BC = 36 см
3) CK = 28.93 см
4) Отрезок MK = 40.5 см
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Где остался единственный экземпляр танка маус...
2 - Мне нужно придумать (повторяю придумать! ) 5 предложений на тему война с дополнениями...
3 - Назовите вещество(фото). составьте структурные формулы 2 изомеров и 2 гомологов...
2 - План добычи руды 1200т за день бригада выполнила 7/9 плана. сколько тонн руды...
3 - Метр стоит 250руб.сколько уйдет денег за 1метр70 см...
2 - Составьте письмо из 21 века в 20 век детям войны...
2 - Постройте углы abc и mnk так чтобы угол abc=120 градусов угол mnk=60градусов...
1 - Вмагазине из 17 кг мандаринов, продано 3 2/5 кг. сколько процентов мандаринов...
2 - Скнижного склада отправили в школы города 28800 учебников. в первую школу отправили...
2 - Синонимы к слову тишина которые оканчиваются на шипящую согласную...
3