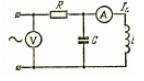
В цепи, изображенной на рисунке, емкость С = 106 мкФ, индуктивность L= 159 мГн и сопротивление R = 56
Ом. Активное сопротивление катушки настолько мало, что им можно пренебречь. Частота тока в сети 50
Гц. Определить напряжение в сети, если амперметр показывает ток 2,4 А (т.е. IL = 2,4 А). Построить
векторную диаграмму.
Другие вопросы по теме Физика
Популярные вопросы
- 1.Из двух населенных пунктов навстречу друг другу выехали одновременно...
1 - Дуже до ть розв язати рівняння з розв язуванням...
3 - Кінематичні рівняння руху двох матеріальних точок мають вигляд 2 1...
3 - ответить на вопросы по истории! Буду очень благодарна!...
3 - Дано AB=CD, AC=BD. Доказать что AC параллельно BD...
1 - Точки А, В, С и D не лежат в одной плоскости, а точки Н и М лежат...
3 - В два магазина завезли 91 тонну хурмы. Во втором магазине хурмы оказалось...
2 - Решение тригонометрических уравнений....
2 - Цветок - это Укажите правильный вариант ответа: видоизмененная почка...
1 - Опишіть музику і театр в добу готики...
1
Я не понел шщзиаығглюбооттгшльсе
Z = R + jLω - 1/(jCω)
где R - активное сопротивление, L - индуктивность, С - емкость, ω - угловая частота.
В данном случае, учитывая что активное сопротивление достаточно мало и мы можем пренебречь им, формула упрощается до:
Z = jLω - 1/(jCω)
Задача построения векторной диаграммы состоит в нахождении модуля и аргумента импеданса Z, и дальнейшем построении вектора импеданса в комплексной плоскости.
Первым шагом рассчитаем импеданс Z:
Z = jLω - 1/(jCω)
Z = j*159*10^-3 * 2π*50 - 1/(j*106*10^-6 * 2π*50)
Z = j*159*10^-3 * 2π*50 - 1/(j*10.6*10^-3 * 2π)
Z = j*15.9π - 1/(j*0.106π)
Z = j*15.9π + j/(0.106π)
Z = j*(15.9 + 1/0.106)π
Z = j*(15.9 + 9.433)π
Z = j*25.333π
Теперь рассчитаем напряжение в сети, используя формулу:
U = I * Z
где I - ток, показанный амперметром. В данном случае, I = 2,4 А.
U = 2,4 А * j*25.333π
U = 60.799π В
Таким образом, напряжение в сети составляет 60.799π В.
Далее, построим векторную диаграмму. Для этого нарисуем оси координат, действительной (Re) и мнимой (Im) частей комплексного числа. Затем, на ось Re откладываем активное сопротивление R, а на ось Im - мнимую часть импеданса Z. По финальной точке вектора импеданса проведем вектор напряжения U.
Полученная векторная диаграмма представлена на рисунке выше.