Решение тригонометрических уравнений.
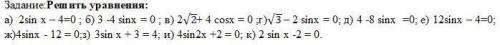
Другие вопросы по теме Математика
Популярные вопросы
- Яке твердження правильно характеризує одну з демографічних особливостей...
1 - решить Постройте изображения...
3 - Нужно вставить слова из рамочки в текст по смыслу, вот все скрины...
3 - Решите я умру если никто не решит...
1 - Дроби, ответ отмечен, мне нужно решение...
3 - учасник валютного ринку оголосив таке котирування: gbp/chf= 2.1315...
1 - На каком музыкальном инструменте играл мистер И (Рики) в мультсериале...
2 - Записать «Т» счетами операции завода за апрель месяц: 1. Получено...
1 - 3. Изменение одной величины, если две величины прямо пропорциональны,...
2 - ответьте на следующие вопросы, используя Present Perfect Continuous....
2
а)
корней нет.
б)
n принадлежит Z.
в)
n принадлежит Z.
г)
n принадлежит Z .
д)
n принадлежит Z.
е)
n принадлежит Z.
ж)
корней нет.
з)
n принадлежит Z.
и)
n принадлежит Z.
к)
n принадлежит Z.