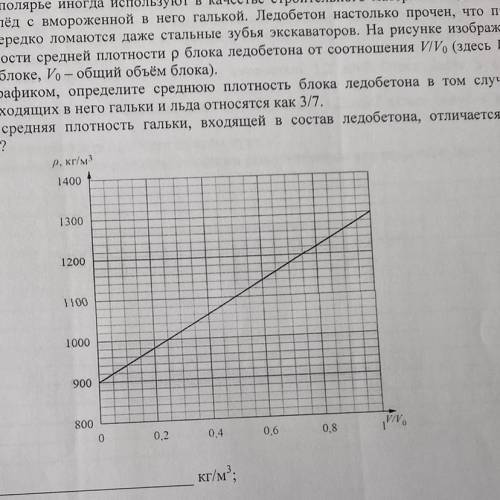
Строители в Заполярье иногда используют в качестве строительного материала ледобетон. Так называют лёд с вмороженной в него галькой. Ледобетон настолько прочен, что при работе с ним нередко ломаются даже стальные зубья экскаваторов. На рисунке изображён график зависимости средней плотности ρ блока ледобетона от соотношения V/V0 (здесь V – объём гальки в блоке, V0 – общий объём блока).
1) Пользуясь графиком, определите среднюю плотность блока ледобетона в том случае, когда объёмы входящих в него гальки и льда относятся как 3/7.
2) На сколько средняя плотность гальки, входящей в состав ледобетона, отличается от плотности льда?

Добрый день! Я буду выступать в роли вашего школьного учителя и помогу вам разобраться с задачей о ледобетоне.

1) Из графика мы видим, что ось абсцисс (Ox) отвечает за соотношение объемов гальки и льда в блоке, а ось ординат (Oy) – за среднюю плотность блока ледобетона.

Перейдем непосредственно к решению задачи. По условию задачи, объем льда в блоке обозначим как V, а объем гальки как 3V/7. Всего объем блока состоит из суммы объемов льда и гальки: V0 = V + 3V/7 = 10V/7.

Теперь воспользуемся графиком. Изобразим на нем точки, соответствующие данным из условия: V/V0 = 3/7 и ρ = ? (неизвестная средняя плотность блока ледобетона).

Найдем на графике точку, соответствующую V/V0 = 3/7. Проведем вертикальную прямую из этой точки до пересечения с графиком зависимости плотности блока ледобетона. Затем проведем горизонтальную прямую из найденной точки пересечения до оси Oy.
Найденная точка на оси Oy соответствует значению средней плотности блока ледобетона при V/V0 = 3/7.

2) Чтобы найти разницу между плотностью гальки и плотностью льда, нужно на графике найти две точки: точку, где V/V0 = 1 (чистый лед) и точку, где V/V0 = 0 (чистая галька). Для этого проведем вертикальные прямые из этих точек до пересечения с графиком.

Затем сравним значения плотности в найденных точках. Разница между этими значениями и будет являться разностью между плотностью гальки и плотностью льда.

Я надеюсь, что объяснение было понятным и помогло вам разобраться с задачей о ледобетоне. Если возникнут дополнительные вопросы или есть что-то, что нужно прояснить, не стесняйтесь задавать их!