1. Физика
  2. По как изменится частота

По как изменится частота колебаний в идеальном колебательном контуре если расстояние между пластинами плоского конденсатора увеличить в два раза?

Nelya2612 Nelya2612    1   03.10.2019 14:50    3

Ответы
ievlevaaleksanra ievlevaaleksanra  09.10.2020 14:32
Дано:

Отношение расстояний между пластинами: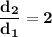 \bf\dfrac{d_2}{d_1} = 2.

Найти нужно отношение частот: \bf\dfrac{\nu_2}{\nu_1} - ?

Решение:

1. Формула Томсона: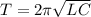 T = 2\pi \sqrt{LC}.

2. Частота через период: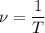 \nu = \dfrac{1}{T}.

3. Формула ёмкости конденсатора: C = \varepsilon \varepsilon_0\dfrac{S}{d}..

4. Учитывая данные формулы, выразим искомое отношение:

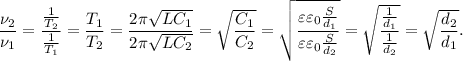
\dfrac{\nu_2}{\nu_1} = \dfrac{\frac{1}{T_2}}{\frac{1}{T_1}} = \dfrac{T_1}{T_2} = \dfrac{2\pi \sqrt{LC_1}}{2\pi \sqrt{LC_2}} = \sqrt{\dfrac{C_1}{C_2}} = \sqrt{\dfrac{\varepsilon \varepsilon_0\frac{S}{d_1}}{\varepsilon \varepsilon_0\frac{S}{d_2}}} = \sqrt{\dfrac{\frac{1}{d_1}}{\frac{1}{d_2}}} = \sqrt{\dfrac{d_2}{d_1}}.

Численно получим:

\dfrac{\nu_2}{\nu_1} = \sqrt{2} или \nu_2 = \sqrt{2}\times\nu_1.

ответ: увеличится в \bf\sqrt{2} раз.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
Neon1407 Neon1407  17.10.2019 17:29
При атмосферном давлении равном 990 гпа. уровень ртути был на 5 см выше её уровня в сосуде, а высота столба воздуха над ртутью была 71 см. при каеом атмосферном давлении...
vlad134631 vlad134631  17.10.2019 17:29
По известным проекциям на оси координат ох и оу определить cosα, если известно: угол α- угол наклона равнодействующей силы f к оси ox ∑ fkx=20кн ∑ fky=15 кн...
utrobin7 utrobin7  17.10.2019 17:30
Решить эти два по с подробным решением.30...
sladkoegka03 sladkoegka03  17.10.2019 17:31
9класс.найти равнодействующую сил f1 =30 н f2=30н f3 =30н​...
ГАЛЯ2006261011444 ГАЛЯ2006261011444  17.10.2019 17:32
Грузовой автомобиль из города а в город б едет 3 часа, а легковой автомобиль 1 час. через сколько часов они встретятся, если одновременно поедут на встречу друг другу?...
Deadsun Deadsun  17.10.2019 17:33
При каком изопроцессе вся теплота сообщенная газу расходуется на работу газа против внешних сил​...
yra221111 yra221111  17.10.2019 15:54
Как зависит внутренняя энергия данной массы идеального газа от его температуры​...
lkQwertyuiop1 lkQwertyuiop1  17.10.2019 15:54
Каким станет заряд двух одинаковых металлических шариков, если их в соприкосновение, а затем развести.первоначальный заряд 1 шарика равен 4е, а второго равен (-6е)?...
tim2k09 tim2k09  17.10.2019 15:54
На рисунке 52а представлен график зависимости равнодействующей всех сил, приложенных к телу, от времени. какой из графиков 52б показывает зависимость скорости этого тела...
CherryGirll CherryGirll  09.09.2019 04:40
При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился, пройдя тормозной путь 50 м. найти ускорение автомобиля при торможении....

Популярные вопросы