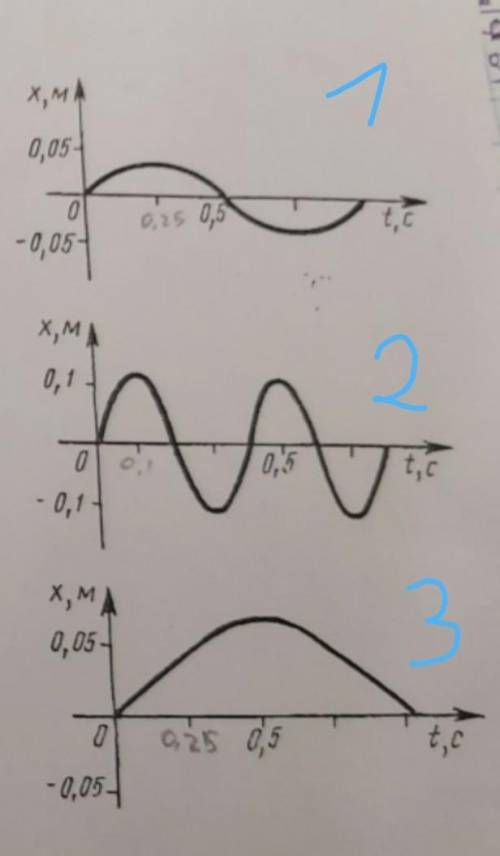
На рисунке представлены графики колебаний трех математических маятников. Укажите, чем отличаются друг от друга колебания этих маятников. Что можно сказать о длинах нитей хтих маятников?
Другие вопросы по теме Физика
Популярные вопросы
- Коло, вписане в трикутник MPN, дотикається до сторони MN в точці С, такій,...
1 - Свойства ГО …………………………………………. В чем суть данного свойства ГО Пример проявления...
1 - : Чим мене зворушує образ Соломії (твір Дорогою ціною) даю 100 б...
3 - Итоги развития Республики Беларусь как суверенного государства Урок обобщения:...
3 - , ЗАВТРА НУЖНО СДАТЬ! С балкона дома, что находится на высоте 8 этажа (24...
2 - Схема процесса окисления :...
3 - A) Teacher: You must walk in the corridors. b)Mother: your homework.c)Boss:...
2 - Что послужило активизации восстание?...
2 - Болотные робинзоны, краткий перессказ. ...
3 - При електролізі розчину солі кадмію виділилося 2 г кадмію. Яка кількість...
3
1) График на верхней панели: на нем представлены колебания маятника с постоянной частотой. Это означает, что время, необходимое для одного полного колебания, у всех точек графика одинаково. Более того, амплитуда (максимальное отклонение от положения равновесия) остается постоянной со временем.
2) График на средней панели: на нем представлены колебания маятника с убывающей частотой. Это означает, что время, необходимое для одного полного колебания, увеличивается со временем. Кроме того, амплитуда убывает со временем, что свидетельствует о затухании колебаний.
3) График на нижней панели: на нем представлены колебания маятника с возрастающей частотой. В этом случае время, необходимое для одного полного колебания, уменьшается со временем. Амплитуда также убывает со временем, что указывает на затухание колебаний.
Теперь давайте обратимся к вопросу о длинах нитей маятников. Длина нити связана с периодом колебаний и частотой маятника. Частота маятника определяется формулой f=1/T, где f - частота, а T - период колебаний. Период колебаний зависит от длины нити по формуле T=2π√(L/g), где L - длина нити, а g - ускорение свободного падения.
Исходя из этих формул, можно сделать предположение о длинах нитей маятников. Мы видим, что у маятника с постоянной частотой (график на верхней панели) время колебаний не меняется, а значит, период сохраняется постоянным. Таким образом, длина нити этого маятника остается неизменной.
У маятника с убывающей частотой (график на средней панели) время колебаний увеличивается и амплитуда убывает. Это может означать, что сила трения действует на маятник и затухает его колебания. В таком случае, трение может привести к увеличению периода колебаний и, следовательно, увеличению длины нити этого маятника.
У маятника с возрастающей частотой (график на нижней панели) время колебаний уменьшается и амплитуда также убывает. Возможно, это свидетельствует о изменении условий, в которых происходят колебания маятника, например, о том, что сила, возвращающая маятник к положению равновесия, увеличивается. В таком случае, сила возвратит маятник к положению равновесия быстрее, и период колебаний уменьшится, что приведет к уменьшению длины нити этого маятника.
Таким образом, на основе анализа графиков колебаний трех математических маятников можно предположить, что длины нитей этих маятников могут различаться.