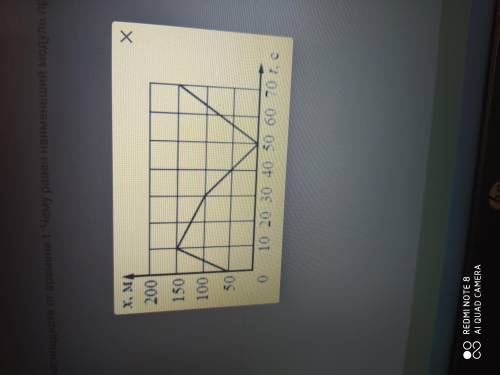
На рисунке представлен график зависимости координаты х велосипедиста от времени t. Чему равен наибольший модуль проекции скорости велосипедиста на ось Ох? ответ выразите в м/с.

Для решения данной задачи, мы должны использовать определение скорости как производной координаты по времени. То есть, в данном случае проекцию скорости велосипедиста на ось Ох можно определить, найдя производную функции координаты х по времени.

Исходя из графика, мы можем заметить, что график представляет функцию, которая изменяется отрицательно в начале и положительно в конце.

Для определения производной функции, мы должны первоначально определить функциональную зависимость графика. В данном случае, у нас нет точных значений, но мы можем примерно приблизить функцию к линейной, так как для определения скорости, в большинстве случаев, используется этот тип зависимости.

Итак, для определения производной функции х по времени, мы должны применить формулу дифференцирования для линейной функции. Формула дифференцирования линейной функции выглядит следующим образом:

dy/dx = k,

где dy/dx - производная функции y по x, а k - коэффициент наклона линейной функции. В данном случае, функция соответствует графику зависимости координаты х велосипедиста от времени t, поэтому можем записать:

dx/dt = k.

Так как нам нужно найти скорость в метрах в секунду (м/с), то необходимо определить значения по осям.

На оси Ох у нас отмечено, что за 5 секунд велосипедист проезжает 250 метров. То есть, значение координаты х увеличивается на 250 метров за 5 секунд. Исходя из этого, мы можем определить значение k:

dx/dt = k = (250 м) / (5 c) = 50 м/с.

Таким образом, скорость велосипедиста по оси Ох составляет 50 м/с, что является наибольшим модулем проекции скорости велосипедиста на данную ось.