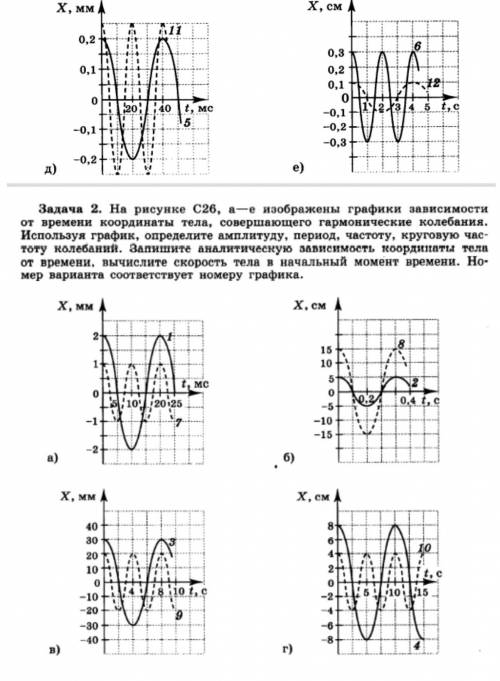
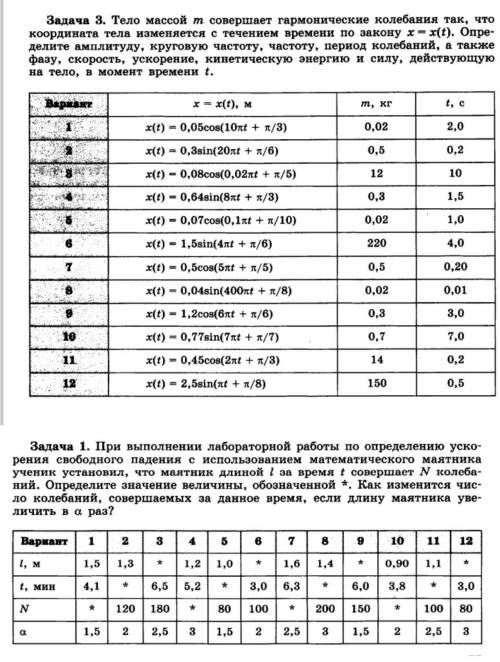
Гармонические колебания ,нужно решить два любых варианта. И подставить значения в следующие задания.

Добрый день!

Для решения данных задач по гармоническим колебаниям, нам потребуются знания о формулах и свойствах гармонических колебаний.

Первое задание:
Рассмотрим гармонические колебания, описываемые следующим уравнением:
x(t) = A*cos(ωt+φ), где x(t) - смещение от положения равновесия в момент времени t, A - амплитуда колебаний, ω - угловая скорость колебаний, φ - начальная фаза.

Задача 1: Найти период колебаний (T) и угловую скорость (ω) гармонических колебаний маятника длиной l=0,8 м.

Для решения данной задачи мы воспользуемся связью между периодом колебаний и угловой скоростью маятника, которая выражается следующей формулой:
T = 2π/ω.

Угловую скорость ω можно определить, используя формулу:
ω = √(g/l), где g - ускорение свободного падения, l - длина маятника.

В данном случае, ускорение свободного падения возьмем равным g = 9,8 м/с^2.

1. Найдем угловую скорость:
ω = √(g/l) = √(9,8 / 0,8) ≈ 3,92 рад/с.

2. Подставим полученное значение угловой скорости в формулу для периода колебаний:
T = 2π/ω = 2π / 3,92 ≈ 1,60 сек.

Таким образом, период колебаний маятника составляет примерно 1,6 сек.

Второе задание:
Задача 2: Найти максимальную скорость (v_max) гармонических колебаний маятника длиной l=1,2 м, если амплитуда колебаний равна A=0,5 м.

Для решения данной задачи воспользуемся связью между максимальной скоростью гармонических колебаний и угловой скоростью, которая выражается следующей формулой:
v_max = A*ω.

1. Найдем угловую скорость:
ω = √(g/l) = √(9,8 / 1,2) ≈ 3,07 рад/с.

2. Подставим полученное значение угловой скорости и амплитуды в формулу для максимальной скорости:
v_max = A*ω = 0,5 * 3,07 ≈ 1,54 м/с.

Таким образом, максимальная скорость колебаний маятника составляет примерно 1,54 м/с.

Надеюсь, ответ ясен и понятен. Если возникли еще вопросы, пожалуйста, обратитесь ко мне!