Две точки движутся по одной окружности с постоянными угловыми скоростями, 0.2 рад/с и 0.3 рад/с. в начальный момент времени угол между радиусами этих точек равен п/3. в какой момент времени вторая догонит первую?

Ответы

ZHICH 03.10.2020 19:00

ответ: c

Объяснение:

Из кинематики мы знаем что координату равномерно и прямолинейно движущегося тела в любой момент времени можно определить из уравнения.

$x(t)=x_{0} +vt$

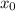Где $x_{0}$ - начальная координата тела

x(t) - координата тела в момент времени

- линейная скорость движения тела

Но можно провести все те же действия по аналогии и вывести формулу для расчета угла поворота тела, в любой момент времени, движущегося с постоянной угловой скоростью по некоторой окружности. В итоге чего получим.

$\phi(t) = \phi_{0} + \omega t$

Где $\phi_{0}$ - начальный угол поворота тела

$\phi(t)$ - угол поворота тела в момент времени

$\omega$ - угловая скорость движения тела

Понятное дело что второе тело догонит первое в тот момент времени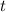 , когда их углы поворотов будут совпадать, то есть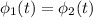 $\phi_{1}(t) = \phi_{2}(t)$

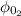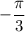Будем считать, что начальный угол поворота первого тела равен нулю, тогда $\phi_{1}(t) = \omega_{1} t$ , а в второго же тела начальный угол поворота $\phi_{0_{2} }$ равен $-\dfrac{\pi }{3}$ рад, тогда $\phi_{2}(t) = \phi_{0_{2}} + \omega_{2} t$

При $\phi_{1}(t) = \phi_{2}(t)$

$\omega_{1} t = \phi_{0_{2}} + \omega_{2} t$ ⇒ $-\phi_{0_{2}} = (\omega_{2}- \omega_{1})t$ , отсюда $t = \dfrac{-\phi_{0_{2}}}{\omega_{2}- \omega_{1}}$