Практическая по Численным методам. Задание 1.
Решить задачу Коши для дифференциального уравнения y’=f(x,y) на отрезке [a;b]
при заданном начальном условии y(a)=y0 и шаге интегрирования h методом
Эйлера:
а) с применением «ручных» вычислений с шагом 2h.
б) с программы для компьютера с шагом h.
в) Свести результаты вычислений в одну таблицу и сопоставить точность
полученных значений функции. Пользуясь таблицей, сделать ручную прикидку
графика интегральной кривой на бумаге.
Задание 2
Решить задачу Коши для дифференциального уравнения y’=f(x,y) на отрезке [a;b]
при заданном начальном условии y(a)=y0 методом Рунге-Кутта с
программы для компьютера с шагом h и с шагом h/2.
На основе результатов двойного счета сделать вывод о точности полученного
решения.
Задание 3
Найти точное решение задачи Коши.
f(x)=xy'-y=y^3
a=0
b=2
y0=0
h=0.2
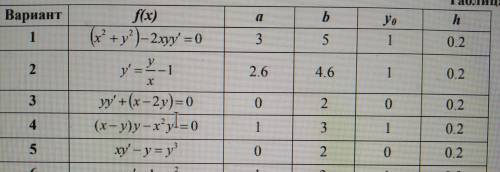
Ответы
Показать ответы (3)
Другие вопросы по теме Другие предметы
Популярные вопросы
- Морфологический разбор словочетания : (построить ракету) *сначала...
2 - На выборах старосты класса 11 человек проголосовало за эмиля ,6 человек...
1 - [9 ] прочитайте слова. сравните произношение и правописание слов....
3 - Вынесите общий множитель за скобки и вычислите значение выражения...
3 - Решите уравнение: a) -0,7x+1,1=-5,2 б) (3-x)(x+2)=0...
1 - Сочинение.если прийти в библиотеку ночью или просто внимательно прислушатьс,...
3 - Ференц лист биография(не много, самую главную суть)...
1 - Два числа относятся как 3: 2.найдите эти числа если их сумма равна...
3 - Нужно ответить на вопрос. значение природы в жизни человека по рассказу...
2 - ответить на пару вопросов ( война и мир) 1. считаете ли вы необходимым...
2