Зобразіть на координатній площині множину точок, координати яких (х;у) задовільняють нерівність 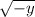

Другие вопросы по теме Алгебра
Популярные вопросы
- Кто написал сказку в дурном обществе...
1 - Найди имена прилагательные день ( ветер ( утро ( воздух ( почки (какие? )...
2 - Морфологический разбор наречия осторожно...
1 - Разбери слова как части речи. ты , вы , видишь , едете надо : (...
1 - Куб с ребром 10 см находится в воде на глубине 15 см. определить силу давления...
3 - 4класс работа решение в магазине есть в продажи мотоцыкл скутер снегоход и квадроцыкл...
3 - Рассчитайте относительную плотность газов кислорода по воздуху желательно с...
2 - При каких натуральных значениях х дробь х/15 будет правильной...
1 - Объясните, почему у греков не было морского флота до греко персидских войн...
3 - Верёвку 28м от неё отрезали 7м . во сколько раз отрезанная часть верёвки меньше...
3
√(–y) ≤ √(1 – x²)
Область допустимых значений: –1 ≤ x ≤ 1, y ≤ 0, поскольку подкоренные выражения не должны быть отрицательными.
Обе части неравенства являются неотрицательными, поэтому их можно возвести в квадрат, чтобы избавиться от корней и переписать неравенство в более удобном виде:
–y ≤ 1 – x² ⇒ y ≥ x² – 1
Построим график параболы y = x² – 1. Решением исходного неравенства √(–y) ≤ √(1 – x²) будут все точки (x; y), лежащие на графике параболы и выше него, при этом попадающие в область допустимых значений. На рисунке множество таких точек изображено фиолетовым цветом (границы области также входят в множество).