Здравствуйте решить понять как решить задачу. Очень сложно, незнакомая для меня тема :((( Буду рада, если срешением большое зарание
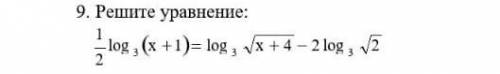
Другие вопросы по теме Алгебра
Популярные вопросы
- Кто первый поднялся на небо1четр2 ведьма...
3 - 5. Закон сталості складу речовин сформулював: а) д. Дальтон;в) д....
3 - Составьте и запишите с именем прилагательным (не)смелый три предложения...
2 - Представте в виде степеней вырожение (сделайте на листке)...
1 - более лёгкие потоки воздуха поднимается вверх у экватора создают...
1 - В равнобедренном треугольнике две стороны равны соответственно 5...
3 - 4. Решите задачу. В аквариум длиной 0,5 м и шириной 20 см налита...
1 - сейчас надо бога дайте ответ...
1 - Длина прямоугольника 1 5/6 см,а ширина. 2 4/9 см Чему равна 2/33...
3 - Задание №1. Прочитайте текст. Передайте содержание близко к тексту....
1
х=0
Объяснение:
логарифм это показатель степени в который надо возвести основание ,чтобы получить логарифмируемое выражение. Если логарифы по ожинаковым основаниям,то сумма логарифмов равна произведению внутренних выражений. разность-деление. Сомножитель перед лог входит в лог в качестве показателя степени. Теперь посмотрим,как преобразуется наше уравнение. Сперва внесем сомножители в степень внутри. дробная степень означает корень степени знаменатели из числа в степени числителя. степень 1/2 означает квадратный корень.
log₃(х+1)¹⁾²= log ₃√(х+4) - log ₃ √2²
log₃√(х+1)= log ₃√(х+4) - log ₃ 2 минус означает деление
log₃√(х+1)= log ₃√(х+4) /2
раз логарифмы равны,значит равны и логарифмируемые выражения
√(х+1)= √(х+4) /2 возводим в квадрат
(х+1)= (х+4) /4
4(х+1)= (х+4)
4х+4=х+4
3х=0
х=0
проверяем log₃(0+1)¹⁾²= log ₃√(0+4) - log ₃ √2²
log₃1= log ₃2 - log ₃ 2 , (3⁰=1) 0=0 все правильно. Если неясно спроси.