Заполнить пропуск. (Теорема Виета) Наше уравнение приведённое 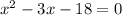, так как а=1.
Значит:
-18<0, множители числа ... в разности равны 3;
3>0, больший по модулю - положительный корень.
Следовательно, x=-6 или x=3.

Добрый день, дорогой ученик! Очень рад, что ты обратился ко мне с этим вопросом. Давайте рассмотрим его подробно и пошагово.

У нас дано уравнение x^2 - 3x - 18 = 0. Это приведённая форма уравнения, где коэффициент перед x^2 равен 1.

Теперь мы хотим использовать Теорему Виета, чтобы заполнить пропуск в задании. В этой теореме говорится, что сумма корней уравнения равна отрицательному коэффициенту перед x, разделённому на коэффициент перед x^2. Также произведение корней равно константе в уравнении, делённой на коэффициент перед x^2.

У нас дано, что сумма корней равна 3 и произведение корней равно -18.

Согласно теореме Виета, мы можем написать систему уравнений:

x1 + x2 = 3
x1 * x2 = -18

Поскольку у нас уже есть одно уравнение, мы можем решить его относительно одной из переменных и подставить это значение во второе уравнение. Давайте решим первое уравнение относительно x1:

x1 = 3 - x2

Теперь мы можем подставить это значение во второе уравнение:

(3 - x2) * x2 = -18

Распишем это уравнение:

3x2 - x2^2 = -18

Теперь приведём уравнение к квадратному виду, где коэффициент перед x^2 будет равен 1. Для этого умножим все члены уравнения на -1:

x2^2 - 3x2 + 18 = 0

Теперь наше уравнение имеет вид x^2 - 3x + 18 = 0. Мы видим, что коэффициент перед x^2 всё ещё равен 1, что удовлетворяет приведённой форме уравнения.

Мы можем применить к этому уравнению дискриминант и найти его корни. Для этого воспользуемся формулой:

x = (-b ± √(b^2 - 4ac)) / (2a)

Здесь a = 1, b = -3, c = 18. Подставим значения и рассчитаем:

x = (-(-3) ± √((-3)^2 - 4*1*18)) / (2*1)
x = (3 ± √(9 - 72)) / 2
x = (3 ± √(-63)) / 2

Теперь у нас есть корень, который является отрицательным числом, а извлечение квадратного корня из отрицательного числа не имеет реальных корней. Поэтому мы не можем найти значение выражения √(-63).

Вернёмся к первому уравнению, где x1 = 3 - x2. Подставим в него значение x = -6:

-6 = 3 - x2

Теперь легко решим это уравнение:

x2 = 3 + 6
x2 = 9

Итак, у нас есть два корня: x = -6 и x = 9.

Надеюсь, что я понятно и подробно объяснил тебе эту задачу. Если у тебя остались какие-либо вопросы, не стесняйся задавать!