, задание на фото,тут тоже уже другое задание
Другие вопросы по теме Алгебра
Популярные вопросы
- Что такое в английском языке специальный вопрос?и как его задать...
3 - Listen again and for each conversation,choose the correct answer A,B or C. There...
3 - Как воевал Александр македонский...
3 - Як читаються ці формули: N2CO3,N2SO3,H2SO4,H3PO4дякую)...
3 - Будет ли напечатано a, если a=7? А если a=20?if a 0 and a 10 or a==100:print(a)...
2 - Луч BD разделил угол ABC на два угла . угол DBC составляет 3/7 от угла ABD. угол...
1 - Сравнительная характеристика химической промышленности Луганщины и России по...
3 - Соотнеси полезные ископаемые и места их добычи. НЕФТЬГАЗЭкибастузТенгизКарачаганакКашаганКарагандыУГОЛЬ...
3 - Это всё одна таблица. Если не сложно Как человека...
2 - Шекспир заканчивает трагедию словами ...но повесть о Ромео и Джульетте останется...
3
Решение.
Применяем свойства степеней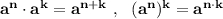 и формулы сокращённого умножения:
и формулы сокращённого умножения: